
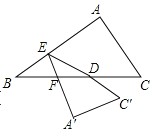
【题目】如图,在Rt△ABC中,AC=3,AB=4,D为斜边BC的中点,E为AB上一个动点,将△ABC沿直线DE折叠,A,C的对应点分别为![]() ,
,![]() ,
,![]() 交BC于点F,若△BEF为直角三角形,则BE的长度为______.
交BC于点F,若△BEF为直角三角形,则BE的长度为______.
【答案】![]() 或
或![]() .
.
【解析】
根据∠B为锐角,分两种情况进行讨论:当∠BEF=90°时,△BEF为直角三角形;当∠BFE=90°时,△BEF为直角三角形,分别根据等腰直角三角形的性质,三角形中位线定理,轴对称的性质以及直角三角形的边角关系进行计算,即可得到BE的长度.
解:分两种情况:
①如图,当∠BEF=90°时,△BEF为直角三角形,
过D作DM⊥AB于M,则∠EMD=90°,DM∥AC,
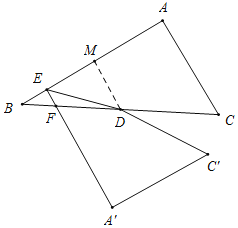
∵D为BC的中点,
∴M为AB的中点,
![]() ,
,
由折叠可得,![]() ,
,
∴△DEM是等腰直角三角形,
![]() ,
,
![]() ;
;
②如图,当∠BFE=90°时,△BEF为直角三角形,
连接AD,A'D,
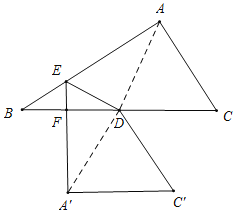
根据对称性可得,∠EAD=∠EA'D,AD=A'D
∵Rt△ABC中,AC=3,AB=4,
∴BC=5,
∵Rt△ABC中,D为BC的中点,
![]() ,
,
∴∠B=∠EAD,
∴∠B=∠FA'D,
设BE=x,则![]() ,
,
![]() ,
,
又∵Rt△A'DF中,sin∠FA'D=sinB,即![]() ,
,
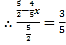 ,
,
解得![]() ,
,
即![]() ,
,
综上所述,BE的长度为![]() 或
或![]() .
.


科目:初中数学 来源: 题型:
【题目】平面内,如图,在□ABCD中,AB=10,AD=15,![]() ,点P为AD边上任意点,连接PB,将PB绕点P逆时针旋转90°得到线段PQ.
,点P为AD边上任意点,连接PB,将PB绕点P逆时针旋转90°得到线段PQ.
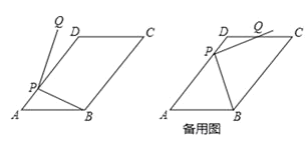
(1)当∠DPQ= 10°时,求∠APB的大小;
(2)当 ![]() 时,求点Q与点B间的距离(结果保留根号);
时,求点Q与点B间的距离(结果保留根号);
(3)若点Q恰好落在口ABCD的边所在的直线上,直接写出PB旋转到PQ所扫过的面积.(结果保留π).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了掌握八年级数学考试卷的命题质量与难度系数,命题组教师赴外地选取一个水平相当的八年级班级进行预测,将考试成绩分布情况进行处理分析,制成频数分布表如下(成绩得分均为整数):
组别 | 成绩分组 | 频数频率 | 频数 |
1 |
| 2 | 0.05 |
2 |
| 4 | 0.10 |
3 |
|
| 0.2 |
4 |
| 10 | 0.25 |
5 |
|
|
|
6 |
| 6 | 0.15 |
合计 | 40 | 1.00 |
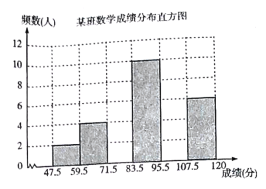
根据表中提供的信息解答下列问题:
(1)频数分布表中的![]() ,
,![]() ,
,![]() ;
;
(2)已知全区八年级共有200个班(平均每班40人),用这份试卷检测,108分及以上为优秀,预计优秀的人数约为 ,72分及以上为及格,预计及格的人数约为 ,及格的百分比约为 ;
(3)补充完整频数分布直方图.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某外国语学校组织九年级学生参加数学、科学、英语竞赛培训,如图两幅统计图反映了学生自愿报名(每人限报一科)的情况,请你根据图中信息回答下列问题:

(1)九年级报名参加三科培训的总人数是_____.
(2)英语学科所占扇形圆心角的度数是_____,请补全上述统计图.
(3)根据实际情况,需从英语组抽调部分同学到数学组,使数学组人数是英语组人数的3倍,则应从英语组抽调多少名学生?
查看答案和解析>>
科目:初中数学 来源: 题型:
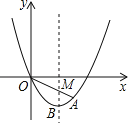
【题目】已知:如图,在平面直角坐标系xOy中,抛物线y=ax2+bx(a≠0)经过点A(6,﹣3),对称轴是直线x=4,顶点为B,OA与其对称轴交于点M,M、N关于点B对称.
(1)求这条抛物线的表达式和点B的坐标;
(2)联结ON、AN,求△OAN的面积;
(3)点Q在x轴上,且在直线x=4右侧,当∠ANQ=45°时,求点Q的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】黄石市在创建国家级文明卫生城市中,绿化档次不断提升.某校计划购进A,B两种树木共100棵进行校园绿化升级,经市场调查:购买A种树木2棵,B种树木5棵,共需600元;购买A种树木3棵,B种树木1棵,共需380元.
(1)求A种,B种树木每棵各多少元?
(2)因布局需要,购买A种树木的数量不少于B种树木数量的3倍.学校与中标公司签订的合同中规定:在市场价格不变的情况下(不考虑其他因素),实际付款总金额按市场价九折优惠,请设计一种购买树木的方案,使实际所花费用最省,并求出最省的费用.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某小区为“创建文明城市,构建和谐社会”.更好的提高业主垃圾分类的意识,业主委员会决定在小区内安装垃圾分类的温馨提示牌和垃圾箱.若购买3个温馨提示牌和4个垃圾箱共需580元,且每个温馨提示牌比垃圾箱便宜40元.
(1)问:购买1个温馨提示牌和1个垃圾箱各需多少元?
(2)如果需要购买温馨提示牌和垃圾箱共10个,费用不超过800元,问:最多购买垃圾箱多少个?
查看答案和解析>>
科目:初中数学 来源: 题型:
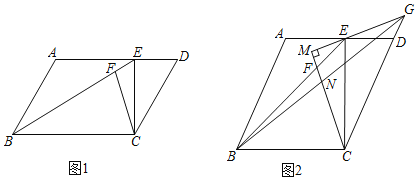
【题目】如图,在平行四边形ABCD中,CE⊥BC交AD于点E,连接BE,点F是BE上一点,连接CF.
(1)如图1,若∠ECD=30°,BC=4,DC=2,求tan∠CBE的值;
(2)如图2,若BC=EC,过点E作EM⊥CF,交CF延长线于点M,延长ME、CD相交于点G,连接BG交CM于点N且CM=MG,
①在射线GM上是否存在一点P,使得△BCP≌△ECG?若存在,请指出点P的位置并证明这对全等三角形;若没有,请说明理由.
②求证:EG=2MN.
查看答案和解析>>
科目:初中数学 来源: 题型:
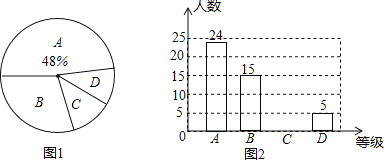
【题目】某销售公司年终进行业绩考核,人事部门把考核结果按照A,B,C,D四个等级,绘制成两个不完整的统计图,如图1,图2.
![]() 参加考试的人数是______,扇形统计图中D部分所对应的圆心角的度数是______,请把条形统计图补充完整;
参加考试的人数是______,扇形统计图中D部分所对应的圆心角的度数是______,请把条形统计图补充完整;
![]() 若公司领导计划从考核人员中选一人交流考核意见,求所选人员考核为A等级的概率;
若公司领导计划从考核人员中选一人交流考核意见,求所选人员考核为A等级的概率;
![]() 为推动公司进一步发展,公司决定计划两年内考核A等级的人数达到30人,求平均每年的增长率
为推动公司进一步发展,公司决定计划两年内考核A等级的人数达到30人,求平均每年的增长率![]() 精确到
精确到![]() ,
,![]()
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com