
 ČēĶ¼£¬Å×ĪļĻßy=-x2-2x+3µÄĶ¼ĻóÓėxÖį½»ÓŚA”¢BĮ½µć£ØµćAŌŚµćBµÄ×ó±ß£©£¬ÓėyÖį½»ÓŚµćC£¬µćDĪŖÅ×ĪļĻߵĶ„µć£®
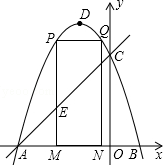
ČēĶ¼£¬Å×ĪļĻßy=-x2-2x+3µÄĶ¼ĻóÓėxÖį½»ÓŚA”¢BĮ½µć£ØµćAŌŚµćBµÄ×ó±ß£©£¬ÓėyÖį½»ÓŚµćC£¬µćDĪŖÅ×ĪļĻߵĶ„µć£®·ÖĪö £Ø1£©ĄūÓĆŗÆŹżĶ¼ĻóÓė×ų±źÖįµÄ½»µćµÄĒó·Ø£¬Ēó³öµćA£¬B£¬CµÄ×ų±ź£»
£Ø2£©ĻČČ·¶Ø³öÅ×ĪļĻ߶Ō³ĘÖį£¬ÓĆm±ķŹ¾³öPM£¬MN¼“æÉ£»
£Ø3£©ÓÉ£Ø2£©µĆµ½µÄ½įĀŪÅŠ¶Ļ³ö¾ŲŠĪÖܳ¤×ī“óŹ±£¬Č·¶Ø³öm£¬½ų¶ųĒó³öÖ±ĻßAC½āĪöŹ½£¬¼“æÉ£»
£Ø4£©ŌŚ£Ø3£©µÄ»ł“”ÉĻ£¬ÅŠ¶Ļ³öNÓ¦ÓėŌµćÖŲŗĻ£¬QµćÓėCµćÖŲŗĻ£¬Ēó³öDQ=DC=$\sqrt{2}$£¬ŌŁ½ØĮ¢·½³Ģ£Øn+3£©-£Ø-n2-2n+3£©=4¼“æÉ£®
½ā“š ½ā£ŗ
£Ø1£©ÓÉÅ×ĪļĻßy=-x2-2x+3æÉÖŖ£¬C£Ø0£¬3£©£®
Įīy=0£¬Ōņ0=-x2-2x+3£¬
½āµĆ£¬x=-3»ņx=l£¬
”ąA£Ø-3£¬0£©£¬B£Ø1£¬0£©£®
£Ø2£©ÓÉÅ×ĪļĻßy=-x2-2x+3æÉÖŖ£¬¶Ō³ĘÖįĪŖx=-1£®
”ßM£Øm£¬0£©£¬
”ąPM=-m2-2m+3£¬MN=£Ø-m-1£©”Į2=-2m-2£¬
”ą¾ŲŠĪPMNQµÄÖܳ¤=2£ØPM+MN£©=£Ø-m2-2m+3-2m-2£©”Į2=-2m2-8m+2£®
£Ø3£©”ß-2m2-8m+2=-2£Øm+2£©2+10£¬
”ą¾ŲŠĪµÄÖܳ¤×ī“óŹ±£¬m=-2£®
”ßA£Ø-3£¬0£©£¬C£Ø0£¬3£©£¬
ÉčÖ±ĻßACµÄ½āĪöŹ½y=kx+b£¬
”ą$\left\{\begin{array}{l}{-3k+b=0}\\{b=3}\end{array}\right.$
½āµĆk=l£¬b=3£¬
”ą½āĪöŹ½y=x+3£¬
Įīx=-2£¬Ōņy=1£¬
”ąE£Ø-2£¬1£©£¬
”ąEM=1£¬AM=1£¬
”ąS=$\frac{1}{2}$AM”ĮEM=$\frac{1}{2}$£®
£Ø4£©”ßM£Ø-2£¬0£©£¬Å×ĪļĻߵĶŌ³ĘÖįĪŖx=-l£¬
”ąNÓ¦ÓėŌµćÖŲŗĻ£¬QµćÓėCµćÖŲŗĻ£¬
”ąDQ=DC£¬
°Ńx=-1“śČėy=-x2-2x+3£¬½āµĆy=4£¬
”ąD£Ø-1£¬4£©£¬
”ąDQ=DC=$\sqrt{2}$£®
”ßFG=2$\sqrt{2}$DQ£¬
”ąFG=4£®
ÉčF£Øn£¬-n2-2n+3£©£¬ŌņG£Øn£¬n+3£©£¬
”ßµćGŌŚµćFµÄÉĻ·½ĒŅFG=4£¬
”ą£Øn+3£©-£Ø-n2-2n+3£©=4£®
½āµĆn=-4»ņn=1£¬
”ąF£Ø-4£¬-5£©»ņ£Ø1£¬0£©£®
µćĘĄ “ĖĢāŹĒ¶ž“ĪŗÆŹż×ŪŗĻĢā£¬Ö÷ŅŖæ¼²éĮĖŗÆŹżĶ¼ĻóÓė×ų±źÖįµÄ½»µćµÄĒó·Ø£¬“ż¶ØĻµŹż·ØĒóŗÆŹż½āĪöŹ½£¬ŗÆŹż¼«ÖµµÄČ·¶Ø£¬½ā±¾ĢāµÄ¹Ų¼üŹĒÓĆm±ķŹ¾³ö¾ŲŠĪPMNQµÄÖܳ¤£®



| Äź¼¶ | øßÖŠæĪ³Ģ | Äź¼¶ | ³õÖŠæĪ³Ģ |
| øßŅ» | øßŅ»Ćā·ŃæĪ³ĢĶĘ¼ö£” | ³õŅ» | ³õŅ»Ćā·ŃæĪ³ĢĶĘ¼ö£” |
| ø߶ž | ø߶žĆā·ŃæĪ³ĢĶĘ¼ö£” | ³õ¶ž | ³õ¶žĆā·ŃæĪ³ĢĶĘ¼ö£” |
| øßČż | øßČżĆā·ŃæĪ³ĢĶĘ¼ö£” | ³õČż | ³õČżĆā·ŃæĪ³ĢĶĘ¼ö£” |
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ½ā“šĢā

²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗŃ”ŌńĢā
| A£® | Čō a”¢b”¢cŹĒ”÷ABCµÄČż±ß£¬Ōņa2+b2=c2 | |
| B£® | Čō a”¢b”¢cŹĒRt”÷ABCµÄČż±ß£¬Ōņa2+b2=c2 | |
| C£® | Čō a”¢b”¢cŹĒRt”÷ABCµÄČż±ß£¬”ĻA=90”ć£¬Ōņa2+b2=c2 | |
| D£® | Čō a”¢b”¢cŹĒRt”÷ABCµÄČż±ß£¬”ĻC=90”ć£¬Ōņa2+b2=c2 |
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗŃ”ŌńĢā
| A£® | x2+4x=10 | B£® | 3x2+8x-3=0 | C£® | x2-2x+3=0 | D£® | £Øx-2£©£Øx-3£©=12 |
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗŃ”ŌńĢā
| A£® | 4£¬5£¬6 | B£® | 1£¬1£¬$\sqrt{2}$ | C£® | 6£¬8£¬11 | D£® | 5£¬12£¬23 |
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗŃ”ŌńĢā
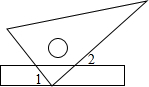 Š”ŗģ°ŃŅ»°ŃÖ±³ßÓėŅ»æéČż½Ē°åČēĶ¼·ÅÖĆ£¬²āµĆ”Ļ1=48”ć£¬Ōņ”Ļ2µÄ¶ČŹżĪŖ£Ø””””£©
Š”ŗģ°ŃŅ»°ŃÖ±³ßÓėŅ»æéČż½Ē°åČēĶ¼·ÅÖĆ£¬²āµĆ”Ļ1=48”ć£¬Ōņ”Ļ2µÄ¶ČŹżĪŖ£Ø””””£©| A£® | 38”ć | B£® | 42”ć | C£® | 48”ć | D£® | 52”ć |
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗŃ”ŌńĢā
| A£® | 64.8”Į104 | B£® | 6.48”Į105 | C£® | 0.648”Į106 | D£® | 6.48”Į106 |
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗŃ”ŌńĢā
| A£® | $\sqrt{2}$+$\sqrt{3}$=$\sqrt{5}$ | B£® | 4$\sqrt{3}$-3$\sqrt{3}$=1 | C£® | $\sqrt{27}$”Ā$\sqrt{3}$=3 | D£® | 2$\sqrt{3}$”Į3$\sqrt{3}$=6 |
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗŃ”ŌńĢā
| A£® | “Ó“ü×ÓÖŠĆž³ö1øöĒņ£¬ĒņµÄŃÕÉ«ŹĒŗģÉ« | |
| B£® | “Ó“ü×ÓÖŠĆž³ö2øöĒņ£¬ĖüĆĒµÄŃÕÉ«ĻąĶ¬ | |
| C£® | “Ó“ü×ÓÖŠĆž³ö3øöĒņ£¬ÓŠŃÕÉ«ĻąĶ¬µÄĒņ | |
| D£® | “Ó“ü×ÓÖŠĆž³ö4øöĒņ£¬ÓŠŃÕÉ«ĻąĶ¬µÄĒņ |
²éæ““š°øŗĶ½āĪö>>
°Ł¶ČÖĀŠÅ - Į·Ļ°²įĮŠ±ķ - ŹŌĢāĮŠ±ķ
ŗž±±Ź”»„ĮŖĶųĪ„·ØŗĶ²»Į¼ŠÅĻ¢¾Ł±ØĘ½ĢØ | ĶųÉĻÓŠŗ¦ŠÅĻ¢¾Ł±Ø×ØĒų | µēŠÅÕ©Ę¾Ł±Ø×ØĒų | É꥜Ź·ŠéĪŽÖ÷ŅåÓŠŗ¦ŠÅĻ¢¾Ł±Ø×ØĒų | ÉęĘóĒÖČؾŁ±Ø×ØĒų
Ī„·ØŗĶ²»Į¼ŠÅĻ¢¾Ł±Øµē»°£ŗ027-86699610 ¾Ł±ØÓŹĻä£ŗ58377363@163.com