
分析 根据勾股定理和锐角三角函数即可解出直角三角形的其他元素.
解答 解:(1)∵∠A=10°,
∴∠B=90°-∠A=80°,
∵sin∠A=$\frac{a}{c}$,
∴c=$\frac{a}{sin10°}$≈46.07,
由勾股定理可求出:b≈45.37;
(2)∵∠B=33°,
∴∠A=90°-∠B=57°,
∵sin∠B=$\frac{b}{c}$,
∴c=$\frac{b}{sin∠B}$≈9.18,
∴由勾股定理可求出:a≈7.70,
(3)∵a=5,c=13,
∴由勾股定理可求出:b=12,
∵sin∠A=$\frac{a}{c}$=$\frac{5}{13}$,
∴∠A≈22.62°,
∴∠B=90°-22.62°=67.38°;
(4)∵c=4$\sqrt{6}$,b=4$\sqrt{2}$.
∴由勾股定理可知:a=8,
∵sin∠A=$\frac{a}{c}$=$\frac{\sqrt{6}}{3}$,
∴∠A≈54.74°,
∴∠B≈35.26°
点评 本题考查解直角三角形,涉及勾股定理,锐角三角函数等知识,属于基础题型.


 同步练习河南大学出版社系列答案
同步练习河南大学出版社系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
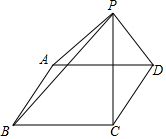 如图,平行四边形ABCD的两个高分别为3cm和4cm,P为平行四边形ABCD外一点,三角形PBC的面积为20cm2,三角形PAD的面积为8cm2,求平行四边形ABCD的周长?
如图,平行四边形ABCD的两个高分别为3cm和4cm,P为平行四边形ABCD外一点,三角形PBC的面积为20cm2,三角形PAD的面积为8cm2,求平行四边形ABCD的周长?查看答案和解析>>
科目:初中数学 来源: 题型:解答题
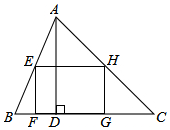 如图,△ABC的内接矩形EFGH,FG在BC上,高AD=20,BC=40,设EF=x,矩形EFGH的面积为y,试求y与x之间的函数关系式,并确定x的取值范围.
如图,△ABC的内接矩形EFGH,FG在BC上,高AD=20,BC=40,设EF=x,矩形EFGH的面积为y,试求y与x之间的函数关系式,并确定x的取值范围.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | ax=ay | B. | x+a=y+a | C. | $\frac{x}{a}$=$\frac{y}{a}$ | D. | $\frac{x}{a+1}$=$\frac{y}{a+1}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图所示的扇形统计图是某商店在第一季度里男、女服装的销售收入情况,由于二月份正值春节,男、女服装的销售收入分别比一月份增长了40%,64%,已知三月份男、女服装的销售总收入为5万元
如图所示的扇形统计图是某商店在第一季度里男、女服装的销售收入情况,由于二月份正值春节,男、女服装的销售收入分别比一月份增长了40%,64%,已知三月份男、女服装的销售总收入为5万元查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com