
 如图,正方形DEFM内接于△ABC,且D、E在AB、AC上,F、M在BC上,∠A=90°,S△CEF═1,S△BMD=4.求S△ABC.
如图,正方形DEFM内接于△ABC,且D、E在AB、AC上,F、M在BC上,∠A=90°,S△CEF═1,S△BMD=4.求S△ABC. 分析 由已知可得△CEF∽△DBM∽△EDA∽△CAB,结合S△CEF═1,S△BMD=4,可得这些三角形两直角边的比,进而求出结论.
解答 解:∵正方形DEFM内接于△ABC,∠A=90°,
可得△CEF∽△DBM∽△EDA∽△CAB,
设CF=x,由S△CEF═1,S△BMD=4,
可得CF:DM=1:2,
∴FE=DE=2x,即$\frac{1}{2}$x•x=1,
∴x=1,
∴CE=$\sqrt{5}$,AE=$\frac{\sqrt{5}}{5}$,
∴AC=$\frac{6\sqrt{5}}{5}$,
∴AB=$\frac{12\sqrt{5}}{5}$,
∴S△ABC=$\frac{1}{2}$AC•AB=$\frac{36}{5}$.
点评 本题主要考查了相似三角形的判定和性质,三角形的面积,勾股定理,解题的关键是证得△CEF∽△DBM∽△EDA∽△CAB.


科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
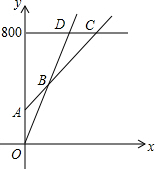 某市游泳馆为了满足不同顾客的需求,设计了三种游泳票:普通票价每次20元/张;金卡售价800元/张,每次凭卡不再收费;银卡售价200元/张,每次凭卡另收10元.这样顾客可根据游泳次数的多少选择不同的消费方式.普通票全年正常出售,两种优惠卡仅限暑期使用,不限次数.设游泳x次时,所需总费用为y元.
某市游泳馆为了满足不同顾客的需求,设计了三种游泳票:普通票价每次20元/张;金卡售价800元/张,每次凭卡不再收费;银卡售价200元/张,每次凭卡另收10元.这样顾客可根据游泳次数的多少选择不同的消费方式.普通票全年正常出售,两种优惠卡仅限暑期使用,不限次数.设游泳x次时,所需总费用为y元.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
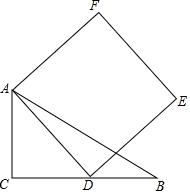 如图.己知△ABC中.∠C=90°,AC=3,BC=4.动点D在边BC上.以AD为边作正方形ADEF.在点D从点C移动至点B的过程中.点E移动的路线长为4$\sqrt{2}$.
如图.己知△ABC中.∠C=90°,AC=3,BC=4.动点D在边BC上.以AD为边作正方形ADEF.在点D从点C移动至点B的过程中.点E移动的路线长为4$\sqrt{2}$.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com