
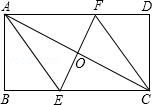
 将矩形ABCD折叠使A,C重合,折痕交BC于E,交AD于F,
将矩形ABCD折叠使A,C重合,折痕交BC于E,交AD于F,分析 (1)根据折叠的性质得OA=OC,EF⊥AC,EA=EC,再利用AD∥AC得到∠FAC=∠ECA,则可根据“ASA”判断△AOF≌△COE,得到OF=OE,加上OA=OC,AC⊥EF,于是可根据菱形的判定方法得到四边形AECF为菱形;
(2)①设菱形的边长为x,则BE=BC-CE=8-x,AE=x,在Rt△ABE中,根据勾股定理得(8-x)2+42=x2,然后解方程即可得到菱形的边长;
②先在Rt△ABC中,利用勾股定理计算出AC=4$\sqrt{5}$,则OA=$\frac{1}{2}$AC=2$\sqrt{5}$,然后在Rt△AOE中,利用勾股定理计算出OE=$\sqrt{5}$,所以EF=2OE=2$\sqrt{5}$.
解答 证明:(1)∵矩形ABCD折叠使A,C重合,折痕为EF,
∴OA=OC,EF⊥AC,EA=EC,
∵AD∥AC,
∴∠FAC=∠ECA,在△AOF和△COE中,
$\left\{\begin{array}{l}{∠FAO=∠ECO}\\{AO=CO}\\{∠AOF=COE}\end{array}\right.$
∴△AOF≌△COE,
∴OF=OE,
∵OA=OC,AC⊥EF,
∴四边形AECF为菱形;
(2)①设菱形的边长为x,则BE=BC-CE=8-x,AE=x,
在Rt△ABE中,∵BE2+AB2=AE2,
∴(8-x)2+42=x2,解得x=5,
即菱形的边长为5;
②在Rt△ABC中,AC=$\sqrt{A{B}^{2}+B{C}^{2}}$=4$\sqrt{5}$,
∴OA=$\frac{1}{2}$AC=2$\sqrt{5}$,
在Rt△AOE中,AE=5,
OE=$\sqrt{A{E}^{2}-A{O}^{2}}$=$\sqrt{5}$,
∴EF=2OE=2$\sqrt{5}$.
点评 此题是折叠问题,主要考查了折叠的性质,全等三角形的判定和性质,菱形的判定和性质,勾股定理,判断出四边形AECF为菱形和求出菱形的边长是解本题的关键.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:选择题
 矩形ABCD中,AD=8cm,AB=6cm.动点E从点C开始沿边CB向点B以2cm/s的速度运动至点B停止,动点F从点C同时出发沿边CD向点D以1cm/s的速度运动至点D停止.如图3可得到矩形CFHE,设运动时间为x(单位:s),此时矩形ABCD去掉矩形CFHE后剩余部分的面积为y(单位:cm2),则y与x之间的函数关系用图象表示大致是图中的( )
矩形ABCD中,AD=8cm,AB=6cm.动点E从点C开始沿边CB向点B以2cm/s的速度运动至点B停止,动点F从点C同时出发沿边CD向点D以1cm/s的速度运动至点D停止.如图3可得到矩形CFHE,设运动时间为x(单位:s),此时矩形ABCD去掉矩形CFHE后剩余部分的面积为y(单位:cm2),则y与x之间的函数关系用图象表示大致是图中的( )| A. |  | B. |  | C. |  | D. |  |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 了解浙江省中学生的视力情况 | |
| B. | 了解九(1)班学生校服的尺码情况 | |
| C. | 检测一批节能灯的使用寿命 | |
| D. | 调查湖州《阿奇讲事体》栏目的收视率 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | $\left\{\begin{array}{l}{x=1}\\{y=3}\end{array}\right.$ | B. | $\left\{\begin{array}{l}{x=-1}\\{y=1}\end{array}\right.$ | C. | $\left\{\begin{array}{l}{x=0}\\{y=-\frac{1}{5}}\end{array}\right.$ | D. | $\left\{\begin{array}{l}{x=-2}\\{y=0}\end{array}\right.$ |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
 甲、乙两人在操场上赛跑,他们赛跑的路程S(m)与时间(min)间的函数关系如图所示,则下列说法中正确的个数有( )
甲、乙两人在操场上赛跑,他们赛跑的路程S(m)与时间(min)间的函数关系如图所示,则下列说法中正确的个数有( )| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 平均数 | B. | 中位数 | C. | 众数 | D. | 方差 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com