
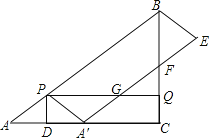
【题目】如图,在Rt△ABC中,∠ACB=90°,AC=8cm,AB=10cm.点P从点A出发,以5cm/s的速度从点A运动到终点B;同时,点Q从点C出发,以3cm/s的速度从点C运动到终点B,连结PQ;过点P作PD⊥AC交AC于点D,将△APD沿PD翻折得到△A′PD,以A′P和PB为邻边作A′PBE,A′E交射线BC于点F,交射线PQ于点G.设A′PBE与四边形PDCQ重叠部分图形的面积为Scm2,点P的运动时间为ts.
(1)当t为何值时,点A′与点C重合;
(2)用含t的代数式表示QF的长;
(3)求S与t的函数关系式;
(4)请直接写出当射线PQ将A′PBE分成的两部分图形的面积之比是1:3时t的值.
【答案】(1)t=1(2)当0<t≤![]() 时,QF=6﹣9t;当
时,QF=6﹣9t;当![]() <t<2时,QF=9t﹣6.
<t<2时,QF=9t﹣6.
当0<t≤![]() 时,S=12t2;当
时,S=12t2;当![]() <t≤1时,S=﹣42t2+72t﹣24:当1<t<2时,S=6t2﹣24t+24.
<t≤1时,S=﹣42t2+72t﹣24:当1<t<2时,S=6t2﹣24t+24.
t的值为![]() 秒或
秒或![]() 秒.
秒.
【解析】
(1)易证△ADP∽△ACB,从而可得AD=4t,由折叠可得AA′=2AD=8t,由点A′与点C重合可得8t=8,从而可以求出t的值.
(2)根据点F的位置不同,可分点F在BQ上(不包括点B)、在CQ上(不包括点Q)、在BC的延长线上三种情况进行讨论,就可解决问题.
(3)根据点F的位置不同,可分点F在BQ上(不包括点B)、在CQ上(不包括点Q)、在BC的延长线上三种情况进行讨论,就可解决问题.
(4)可分①S△A′PG:S四边形PBEG=1:3,如图7,②S△BPN:S四边形PNEA′=1:3,如图8,两种情况进行讨论,就可解决问题.
试题
试题解析:(1)如图1,
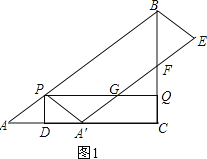
由题可得:PA′=PA=5t,CQ=3t,AD=A′D.
∵∠ACB=90°,AC=8,AB=10,∴BC=6.
∵∠ADP=∠ACB=90°,
∴PD∥BC.
∴△ADP∽△ACB.
∴![]() .
.
∴![]() .
.
∴AD=4t,PD=3t.
∴AA′=2AD=8t.
当点A′与点C重合时,AA′=AC.
∴8t=8.
∴t=1.
(2)①当点F在线段BQ上(不包括点B)时,如图1,
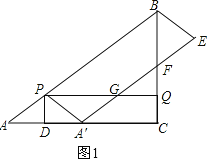
则有CQ≤CF<CB.
∵四边形A′PBE是平行四边形,
∴A′E∥BP.
∴△CA′F∽△CAB.
∴![]() .
.
∴![]() .
.
∴CF=6﹣6t.
∴3t≤6﹣6t<6.
∴0<t≤![]() .
.
此时QF=CF﹣CQ=6﹣6t﹣3t=6﹣9t.
②当点F在线段CQ上(不包括点Q)时,如图2,
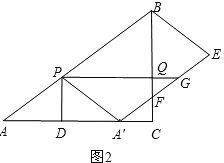
则有0≤CF<CQ.
∵CF=6﹣6t,CQ=3t,
∴0≤6﹣6t<3t.
∴![]() <t≤1.
<t≤1.
此时QF=CQ﹣CF=3t﹣(6﹣6t)=9t﹣6.
③当点F在线段BC的延长线上时,如图3,
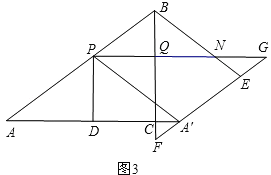
则有AA′>AC,且AP<AB.
∴8t>8,且5t<10.
∴1<t<2.
同理可得:CF=6t﹣6.
此时QF=QC+CF=3t+6t﹣6=9t﹣6.
综上所述:当0<t≤![]() 时,QF=6﹣9t;当
时,QF=6﹣9t;当![]() <t<2时,QF=9t﹣6.
<t<2时,QF=9t﹣6.
(3)①当0<t≤![]() 时,
时,
过点 A′作A′M⊥PG,垂足为M,如图4,
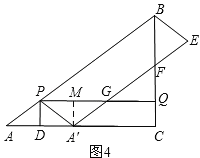
则有A′M=CQ=3t.
∵![]() ,
,![]()
∴![]()
![]() ,
,
∵∠PBQ=∠ABC,
∴△BPQ∽△BAC.
∴∠BQP=∠BCA.
∴PQ∥AC.
∵AP∥A′G.
∴四边形APGA′是平行四边形.
∴PG=AA′=8t.
∴S=S△A′PG=![]() PGA′M
PGA′M
=![]() ×8t×3t=12t2.
×8t×3t=12t2.
②当![]() <t≤1时,
<t≤1时,
过点 A′作A′M⊥PG,垂足为M,如图5,
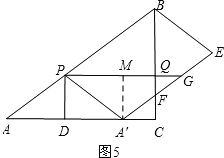
则有A′M=QC=3t,PQ=DC=8﹣4t,PG=AA′=8t,QG=PG﹣PQ=12t﹣8,QF=9t﹣6..
∴S=S△A′PG﹣S△GQF
=![]() PGA′M﹣
PGA′M﹣![]() QGQF
QGQF
=![]() ×8t×3t﹣
×8t×3t﹣![]() ×(12t﹣8)×(9t﹣6)
×(12t﹣8)×(9t﹣6)
=﹣42t2+72t﹣24.
③当1<t<2时,如图6,
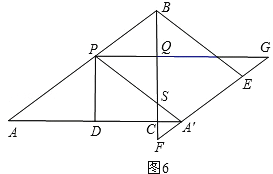
∵PQ∥AC,PA=PA′
∴∠BPQ=∠PAA′,∠QPA′=∠PA′A,∠PAA′=∠PA′A.
∴∠BPQ=∠QPA′.
∵∠PQB=∠PQS=90°,
∴∠PBQ=∠PSQ.
∴PB=PS.
∴BQ=SQ.
∴SQ=6﹣3t.
∴S=S△PQS=![]() PQQS=
PQQS=![]() ×(8﹣4t)×(6﹣3t)=6t2﹣24t+24.
×(8﹣4t)×(6﹣3t)=6t2﹣24t+24.
综上所述:当0<t≤![]() 时,S=12t2;当
时,S=12t2;当![]() <t≤1时,S=﹣42t2+72t﹣24:当1<t<2时,S=6t2﹣24t+24.
<t≤1时,S=﹣42t2+72t﹣24:当1<t<2时,S=6t2﹣24t+24.
(4)①若S△A′PG:S四边形PBEG=1:3,
过点A′作A′M⊥PG,垂足为M,过点A′作A′T⊥PB,垂足为T,如图7,
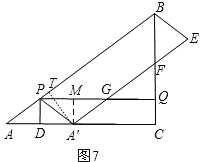
则有A′M=PD=QC=3t,PG=AA′=8t.
∴S△A′PG=![]() ×8t×3t=12t2.
×8t×3t=12t2.
∵S△APA′=![]() APA′T=
APA′T=![]() AA′PD,
AA′PD,
∴A′T=![]()
∴SPBEA′=PBA′T=(10﹣5t)×![]() =24t(2﹣t).
=24t(2﹣t).
∵S△A′PG:S四边形PBEG=1:3,
∴S△A′PG=![]() ×SPBEA′.
×SPBEA′.
∴12t2=![]() ×24t(2﹣t).
×24t(2﹣t).
∵t>0,
<>∴t=②若S△BPN:S四边形PNEA′=1:3,如图8,
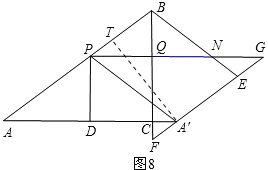
同理可得:∠BPQ=∠A′PQ,BQ=6﹣3t,PQ=8﹣4t,SPBEA′=24t(2﹣t).
∵四边形PBEA′是平行四边形,
∴BE∥PA′.
∴∠BNP=∠NPA′.
∴∠BPN=∠BNP.
∴BP=BN.
∵∠BQP=∠BQN=90°,
∴PQ=NQ.
∴S△BPN=![]() PNBQ=PQBQ
PNBQ=PQBQ
=(8﹣4t)×(6﹣3t).
∵S△BPN:S四边形PNEA′=1:3,
∴S△BPN=![]() ×SPBEA′.
×SPBEA′.
∴(8﹣4t)×(6﹣3t)=![]() ×24t(2﹣t).
×24t(2﹣t).
∵t<2,
∴t=![]() .
.
综上所述:当射线PQ将A′PBE分成的两部分图形的面积之比是1:3时,t的值为![]() 秒或
秒或![]() 秒.
秒.


 状元及第系列答案
状元及第系列答案 同步奥数系列答案
同步奥数系列答案科目:初中数学 来源: 题型:
【题目】山西省每年的体育考试分成必考科目与选考科目两部分.其中选考科目是从一分钟跳绳、掷实心球、坐位体前屈、仰卧起坐四个项目中选取一项.王红与李丽是一对好朋友且都在2020年参加中考,实心球是她俩的弱项,其他三项都非常强,体育考试选考的四个项目中,她俩一定不会选实心球.
(1)王红在选考项目中,选中坐位体前屈的概率是 .
(2)王红与李丽选取同一个选考项目的概率是多少? (在画树状图或列表时,“一分钟跳绳"用“![]() ”表示,“坐位体前屈”用“
”表示,“坐位体前屈”用“![]() "表示,“仰卧起坐”用“
"表示,“仰卧起坐”用“![]() ”表示,“掷实心球”用“
”表示,“掷实心球”用“![]() ”表示)
”表示)
(3)通过对我省某市2020年参加中考的学生进行随机调查,发现该市选择“坐位体前屈”的学生的频率稳定在![]() 左右,已知该市有
左右,已知该市有![]() 人参加2020年中考体育,请由此估计该市这
人参加2020年中考体育,请由此估计该市这![]() 名学生中选择“坐位体前屈”的人数.
名学生中选择“坐位体前屈”的人数.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】我们把两边之比为整数的三角形称为倍比三角形.其中,这个整数比称为倍比,第三条边叫做该三角形的底.
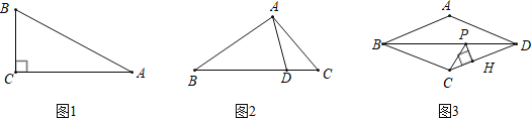
(1)如图1,△ABC是以AC为底的倍比三角形,倍比为3,若∠C=90°,AC=2![]() ,求BC的长;
,求BC的长;
(2)如图2,△ABC中,D为BC边上一点,BD=3,CD=1,连结AD.若AC=2,求证:△ABD是倍比三角形,并求出倍比;
(3)如图3,菱形ABCD中,∠BAD为钝角,P为对角线BD上一动点,过P作PH⊥CD于H、当CP+PH的值最小时,APCD恰好是以PD为底的倍比三角形,记倍比为x,![]() =y,求y关于x的函数关系式.
=y,求y关于x的函数关系式.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角标系中,抛物线C:y=![]() 与x轴交于A、B两点(点A在点B的左侧),与y轴交于点C,点D为y轴正半轴上一点.且满足OD=
与x轴交于A、B两点(点A在点B的左侧),与y轴交于点C,点D为y轴正半轴上一点.且满足OD=![]() OC,连接BD,
OC,连接BD,
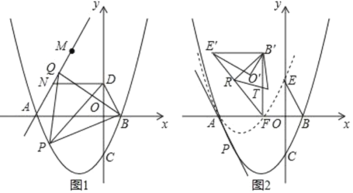
(1)如图1,点P为抛物线上位于x轴下方一点,连接PB,PD,当S△PBD最大时,连接AP,以PB为边向上作正△BPQ,连接AQ,点M与点N为直线AQ上的两点,MN=2且点N位于M点下方,连接DN,求DN+MN+![]() AM的最小值
AM的最小值
(2)如图2,在第(1)问的条件下,点C关于x轴的对称点为E,将△BOE绕着点A逆时针旋转60°得到△B′O′E′,将抛物线y=![]() 沿着射线PA方向平移,使得平移后的抛物线C′经过点E,此时抛物线C′与x轴的右交点记为点F,连接E′F,B′F,R为线段E’F上的一点,连接B′R,将△B′E′R沿着B′R翻折后与△B′E′F重合部分记为△B′RT,在平面内找一个点S,使得以B′、R、T、S为顶点的四边形为矩形,求点S的坐标.
沿着射线PA方向平移,使得平移后的抛物线C′经过点E,此时抛物线C′与x轴的右交点记为点F,连接E′F,B′F,R为线段E’F上的一点,连接B′R,将△B′E′R沿着B′R翻折后与△B′E′F重合部分记为△B′RT,在平面内找一个点S,使得以B′、R、T、S为顶点的四边形为矩形,求点S的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】综合与探究:
已知二次函数y=﹣![]() x2+
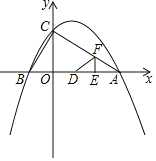
x2+![]() x+2的图象与x轴交于A,B两点(点B在点A的左侧),与y轴交于点C.
x+2的图象与x轴交于A,B两点(点B在点A的左侧),与y轴交于点C.
(1)求点A,B,C的坐标;
(2)求证:△ABC为直角三角形;
(3)如图,动点E,F同时从点A出发,其中点E以每秒2个单位长度的速度沿AB边向终点B运动,点F以每秒![]() 个单位长度的速度沿射线AC方向运动.当点F停止运动时,点E随之停止运动.设运动时间为t秒,连结EF,将△AEF沿EF翻折,使点A落在点D处,得到△DEF.当点F在AC上时,是否存在某一时刻t,使得△DCO≌△BCO?(点D不与点B重合)若存在,求出t的值;若不存在,请说明理由.
个单位长度的速度沿射线AC方向运动.当点F停止运动时,点E随之停止运动.设运动时间为t秒,连结EF,将△AEF沿EF翻折,使点A落在点D处,得到△DEF.当点F在AC上时,是否存在某一时刻t,使得△DCO≌△BCO?(点D不与点B重合)若存在,求出t的值;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某果园的工人需要摘苹果园和梨园的果实,苹果园的果实是梨园的![]() 倍,如果前三天工人都在苹果园摘果实,第四天,
倍,如果前三天工人都在苹果园摘果实,第四天,![]() 的工人到梨园摘果实,剩下
的工人到梨园摘果实,剩下![]() 的工人仍在苹果园摘果实,则第四天结束后苹果园的果实全部摘完,梨园剩下的果实正好是
的工人仍在苹果园摘果实,则第四天结束后苹果园的果实全部摘完,梨园剩下的果实正好是![]() 名工人
名工人![]() 天的工作量.如果前三天工人都在苹果园摘果实,要使苹果和梨同时摘完,则第四天开始,再外请一个工人的情况下,应该安排___人摘苹果.(假定工人们每人每天摘果实的数量是相等的,且每人每天的工作时间相等)
天的工作量.如果前三天工人都在苹果园摘果实,要使苹果和梨同时摘完,则第四天开始,再外请一个工人的情况下,应该安排___人摘苹果.(假定工人们每人每天摘果实的数量是相等的,且每人每天的工作时间相等)
查看答案和解析>>
科目:初中数学 来源: 题型:
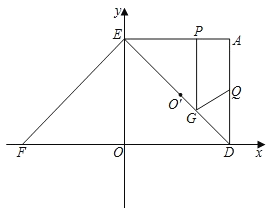
【题目】如图,等腰直角△OEF在坐标系中,有E(0,2),F(﹣2,0),将直角△OEF绕点E逆时针旋转90°得到△ADE,且A在第一象限内,抛物线y=ax2+bx+c经过点A,E.且2a+3b+5=0.
(1)求抛物线的解析式.
(2)过ED的中点O'作O'B⊥OE于B,O'C⊥OD于C,求证:OBO'C为正方形.
(3)如果点P由E开始沿EA边以每秒2厘米的速度向点A移动,同时点Q由点A沿AD边以每秒1厘米的速度向点D移动,当点P移动到点A时,P,Q两点同时停止,且过P作GP⊥AE,交DE于点G,设移动的开始后为t秒.
①若S=PQ2(厘米),试写出S与t之间的函数关系式,并写出t的取值范围?
②当S取最小时,在抛物线上是否存在点R,使得以P,A,Q,R为顶点的四边形是平行四边形?如果存在,求出R的坐标;如果不存在,请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com