
 =1.73)
=1.73)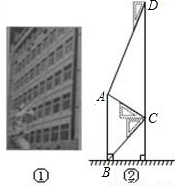
 解:过点C作CE⊥AB于E.
解:过点C作CE⊥AB于E. CD=5.
CD=5. AC=
AC= ,
, .
. ,
, ≈6.8(米).
≈6.8(米).

科目:初中数学 来源: 题型:
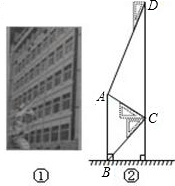 腾飞中学在教学楼前新建了一座“腾飞”雕塑(如图①).为了测量雕塑的高度,小明在二楼找到一点C,利用三角板测得雕塑顶端A点的仰角为30°,底部B点的俯角为45°,小华在五楼找到一点D,利用三角板测得A点的俯角为60°(如图②).若已知CD为10米,请求出雕塑AB的高度.(结果精确到0.1米,参考数据
腾飞中学在教学楼前新建了一座“腾飞”雕塑(如图①).为了测量雕塑的高度,小明在二楼找到一点C,利用三角板测得雕塑顶端A点的仰角为30°,底部B点的俯角为45°,小华在五楼找到一点D,利用三角板测得A点的俯角为60°(如图②).若已知CD为10米,请求出雕塑AB的高度.(结果精确到0.1米,参考数据| 3 |
查看答案和解析>>
科目:初中数学 来源: 题型:
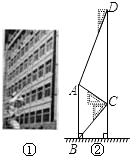 腾飞中学在教学楼前新建了一座“腾飞”雕塑(如Z图①).为了测量雕塑的高度,小明在二楼找到一点C,利用三角板测得雕塑顶端A点的仰角为30°,底部B点的俯角为45°,小华在五楼找到一点D,利用三角板测得A点的俯角为60°(如图②).若已知CD为12米,请求出雕塑AB的高度.(结果精确到0.1米,参考数据
腾飞中学在教学楼前新建了一座“腾飞”雕塑(如Z图①).为了测量雕塑的高度,小明在二楼找到一点C,利用三角板测得雕塑顶端A点的仰角为30°,底部B点的俯角为45°,小华在五楼找到一点D,利用三角板测得A点的俯角为60°(如图②).若已知CD为12米,请求出雕塑AB的高度.(结果精确到0.1米,参考数据| 3 |
查看答案和解析>>
科目:初中数学 来源: 题型:
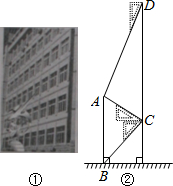 腾飞中学在教学楼前新建了一座“腾飞”雕塑(如图①).为了测量雕塑的高度,小明在二楼找到一点C,利用三角板测得雕塑顶端A点的仰角为30°,底部B点的俯角为45°,小华在五楼找到一点D,利用三角板测得A点的俯角为60°(如图②).若已知CD为10米,请求出雕塑AB的高度.(结果精确到0.1米,参考数据
腾飞中学在教学楼前新建了一座“腾飞”雕塑(如图①).为了测量雕塑的高度,小明在二楼找到一点C,利用三角板测得雕塑顶端A点的仰角为30°,底部B点的俯角为45°,小华在五楼找到一点D,利用三角板测得A点的俯角为60°(如图②).若已知CD为10米,请求出雕塑AB的高度.(结果精确到0.1米,参考数据| 3 |
查看答案和解析>>
科目:初中数学 来源: 题型:
腾飞中学在教学楼前新建了一座“腾飞”雕塑(如图①).为了测量雕塑的高度,小明在二楼找到一点C,利用三角板测得雕塑顶端A点的仰角为![]() ,底部B点的俯角为
,底部B点的俯角为![]() ,小华在五楼找到一点D,利用三角板测得A点的俯角为
,小华在五楼找到一点D,利用三角板测得A点的俯角为![]() (如图②).若已知CD为12米,请求出雕塑AB的高度.(结果精确
(如图②).若已知CD为12米,请求出雕塑AB的高度.(结果精确
到0.1米,参考数据![]() )
)

查看答案和解析>>
科目:初中数学 来源:2012届度河北北城中学初三第一学期期末数学试卷 题型:解答题
腾飞中学在教学楼前新建了一座“腾飞”雕塑(如图①).为了测量雕塑的高度,小明在二楼找到一点C,利用三角板测得雕塑顶端A点的仰角为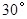 ,底部B点的俯角为
,底部B点的俯角为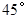 ,小华在五楼找到一点D,利用三角板测得A点的俯角为
,小华在五楼找到一点D,利用三角板测得A点的俯角为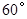 (如图②).若已知CD为12米,请求出雕塑AB的高度.(结果精确
(如图②).若已知CD为12米,请求出雕塑AB的高度.(结果精确
到0.1米,参考数据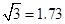 )
)

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com