
【题目】为了解全校学生上学的交通方式,我校九年级(21)班的5名同学联合设计了一份调查问卷,对该校部分学生进行了随机调查.按A(骑自行车)、B(乘公交车)、C(步行)、D(乘私家车)、E(其他方式)设置选项,要求被调查同学从中单选.并将调查结果绘制成条形统计图1和扇形统计图2,根据以上信息,解答下列问题:
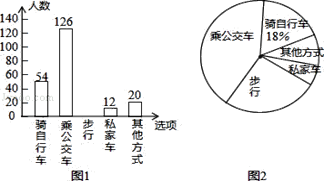
(1)本次接受调查的总人数是 人,其中“步行”的人数是 人;
(2)在扇形统计图中,“乘公交车”的人数所占的百分比是 ,“其他方式”所在扇形的圆心角度数是 ;
(3)已知这5名同学中有2名女同学,要从中选两名同学汇报调查结果.请你用列表法或画树状图的方法,求出恰好选出1名男生和1名女生的概率.
【答案】(1) 300,88;(2)42%,24°;(3)![]() .
.
【解析】试题分析:(1)用骑自行车的人数除以它所占的百分比即可得到调查的总人数,再用总人数-骑自行车的人数-乘公交车的人数-私家车的人数-其他方式的人数即可得到“步行”的人数;
(2)用“乘公交车”的人数÷总人数即可得到其所占的百分比,用“其他方式”的人数÷总人数再乘以360°得到“其他方式”所在扇形的圆心角度数;
(3)先画树状图展示所有20种等可能的结果数,再找出选出1名男生和1名女生的结果数,然后根据概率公式求解.
试题解析:解:(1)本次接受调查的总人数为54÷18%=300(人),“步行”的人数=300-54-126-12-20=88(人);
(2)“乘公交车”的人数所占的百分比是=![]() =42%;扇形统计图中“其他方式”所在扇形的圆心角度数为
=42%;扇形统计图中“其他方式”所在扇形的圆心角度数为![]() ×360°=24°;
×360°=24°;
(3)画树状图为:

共有20种等可能的结果数,其中选出1名男生和1名女生的结果数为12种,所以恰好选出1名男生和1名女生的概率=![]() =
=![]() .
.


 优生乐园系列答案
优生乐园系列答案科目:初中数学 来源: 题型:
【题目】如图正方形ABCD中,点E、F分别在CD、BC边上,△AEF是等边三角形.以下结论:①EC=FC;②∠AED=75°;③AF=![]() CE;④EF的垂直平分线是直线AC.正确结论个数有( )个.
CE;④EF的垂直平分线是直线AC.正确结论个数有( )个.

A. 1B. 2C. 3D. 4
查看答案和解析>>
科目:初中数学 来源: 题型:
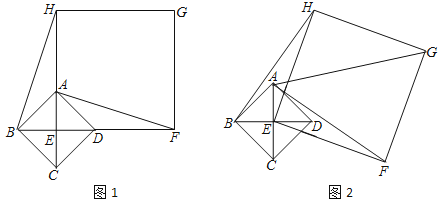
【题目】如图1,已知四边形ABCD是正方形,对角线AC、BD相交于点E,以点E为顶点作正方形EFGH.
(1)如图1,点A、D分别在EH和EF上,连接BH、AF,BH和AF有何数量关系,并说明理由;
(2)将正方形EFGH绕点E顺时针方向旋转,如图2,判断BH和AF的数量关系,并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某地为了解青少年实力情况,现随机抽查了若干名初中学生进行视力情况统计,分为视力正常、轻度近视、重度近视三种情况,并绘成如图所示的条形统计图和扇形统计图(不完整),请你根据图中信息解答下列问题:
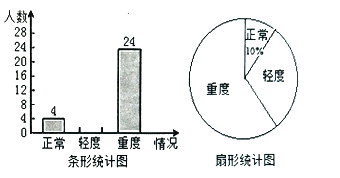
(1)求这次被抽查的学生一共有多少人?
(2)求被抽查的学生中轻度近视的学生人数,并将条形统计图补充完整;
(3)若某地有![]() 万名初中生,请估计视力不正常(包括轻度近视、重度近视)的学生共有多少人?
万名初中生,请估计视力不正常(包括轻度近视、重度近视)的学生共有多少人?
查看答案和解析>>
科目:初中数学 来源: 题型:
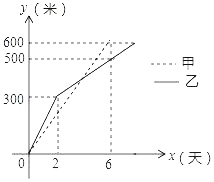
【题目】甲、乙两工程队分别同时开挖两条600米长的管道,所挖管道长度y(单位:米)与挖掘时间x(单位:天)之间的关系如图所示,则下列说法中:①甲队每天挖100米;②乙队开挖两天后,每天挖50米;③当x=4时,甲、乙两队所挖管道长度相同;④甲队比乙队提前2天完成任务.正确的是_____(直接填序号).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,抛物线y=ax2+bx+c的顶点为B(1,﹣3),与x轴的一个交点A在(2,0)和(3,0)之间,下列结论中:①bc>0;②2a+b=0;③a﹣b+c>0;④a﹣c=3,正确的有( )个
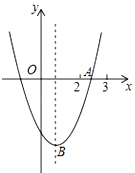
A. 4 B. 3 C. 2 D. 1
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,![]() ,点
,点![]() 是直线
是直线![]() 、
、![]() 之间的一点,连接
之间的一点,连接![]() 、
、![]() .
.
(1)问题发现:
①若![]() ,
,![]() ,则
,则![]() ___________.
___________.
②猜想图1中![]() 、
、![]() 、
、![]() 的数量关系,并证明你的结论.
的数量关系,并证明你的结论.
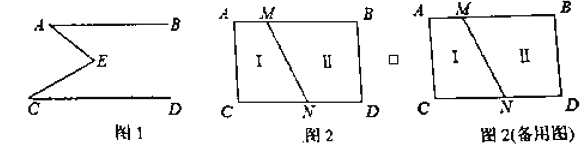
(2)拓展应用:
如图2,![]() ,线段
,线段![]() 把
把![]() 这个封闭区域分为Ⅰ、Ⅱ两部分(不含边界),点
这个封闭区域分为Ⅰ、Ⅱ两部分(不含边界),点![]() 是位于这两个区域内的任意一点,请直接写出
是位于这两个区域内的任意一点,请直接写出![]() 、
、![]() 、
、![]() 的数量关系.
的数量关系.
查看答案和解析>>
科目:初中数学 来源: 题型:
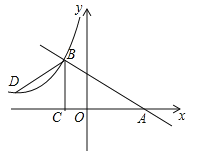
【题目】如图,已知一次函数y=kx+b的图象与x轴交于点A,与反比例函数![]() (x<0)的图象交于点B(﹣2,n),过点B作BC⊥x轴于点C,点D(3﹣3n,1)是该反比例函数图象上一点.
(x<0)的图象交于点B(﹣2,n),过点B作BC⊥x轴于点C,点D(3﹣3n,1)是该反比例函数图象上一点.
(1)求m的值;
(2)若∠DBC=∠ABC,求一次函数y=kx+b的表达式.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】认真阅读下面的材料,完成有关问题.
材料:在学习绝对值时,老师教过我们绝对值的几何含义,一般地,点A、B在数轴上分别表示有理数a、b,那么A、B之间的距离可表示为|a﹣b|.
问题(1):点A、B、C在数轴上分别表示有理数x、﹣2、1,那么A到B的距离与A到C的距离之和可表示为 (用含绝对值的式子表示).
问题(2):利用数轴探究:①找出满足|x﹣3|+|x+1|=6的x的所有值是 ;
②设|x﹣3|+|x+1|=p,当x的值取在不小于﹣1且不大于3的范围时,p的值是不变的,而且是p的最小值,这个最小值是 ;当x的值取在 的范围时,|x|+|x﹣2|的最小值是 .
问题(3):求|x﹣3|+|x﹣2|+|x+1|的最小值以及此时x的值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com