
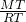 为定值.上述结论有且只有一个是正确的,请选择你认为正确的结论度证明求值.
为定值.上述结论有且只有一个是正确的,请选择你认为正确的结论度证明求值.
 ,b=-
,b=- ,
, x2-x-
x2-x- ;
;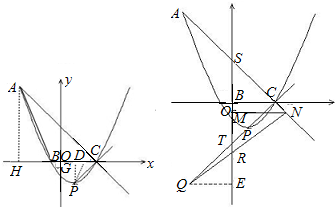
 x2-x-
x2-x- ,令y=0,
,令y=0, x2-x-
x2-x- =0,解得x1=-1,x2=3,
=0,解得x1=-1,x2=3, x2-x-
x2-x- =
= (x-1)2-2,
(x-1)2-2, AH=6
AH=6 ,PC=
,PC= PG=2
PG=2 ,
, :6
:6 ,
, ,
, =
= ,
, ,0);
,0); SC=
SC=
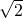 BC=6,MN=MS=3+t,
BC=6,MN=MS=3+t, ME=3,即MR的长度不变;
ME=3,即MR的长度不变;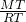 =
=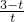 ,即
,即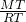 随t的变化而变化.
随t的变化而变化. AH=6
AH=6 ,PC=
,PC= PG=2
PG=2 ,满足∠DPC=∠BAC,则△DPC∽△BAC,利用相似比计算出CD,在计算出OD,即可得到点D的坐标.
,满足∠DPC=∠BAC,则△DPC∽△BAC,利用相似比计算出CD,在计算出OD,即可得到点D的坐标. SC=
SC=
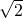 BC=6,MN=MS=3+t,得OT=3,MT=3-t;易证Rt△TQE≌Rt△SNM,得到QE=MN=3+t,则RM=RE,TE=QE=3+t,可求出ME=MT+TE=3-t+3+t=6,从而得到MR=
BC=6,MN=MS=3+t,得OT=3,MT=3-t;易证Rt△TQE≌Rt△SNM,得到QE=MN=3+t,则RM=RE,TE=QE=3+t,可求出ME=MT+TE=3-t+3+t=6,从而得到MR= ME=3,即MR的长度不变.
ME=3,即MR的长度不变.

 期末1卷素质教育评估卷系列答案
期末1卷素质教育评估卷系列答案科目:初中数学 来源: 题型:
 与x轴的另一个交点为E.
与x轴的另一个交点为E.查看答案和解析>>
科目:初中数学 来源: 题型:
 如图,已知抛物线y=ax2+bx+c(其中b>0,c<0)的顶点P在x轴上,与y轴交于点Q,过坐标原点O,作OA⊥PQ,垂足为A,且OA=
如图,已知抛物线y=ax2+bx+c(其中b>0,c<0)的顶点P在x轴上,与y轴交于点Q,过坐标原点O,作OA⊥PQ,垂足为A,且OA=| 2 |
查看答案和解析>>
科目:初中数学 来源: 题型:
| c | a |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com