【题目】如图，在△ABC和△ADE中，AB=AC，AD=AE，且∠BAC=∠DAE，点E在BC上．过点D作DF∥BC，连接DB．
求证：（1）△ABD≌△ACE；
（2）DF=CE．
【答案】（1）证明见解析；（2）证明见解析.
【解析】
（1）求出∠BAD=∠BAC，根据SAS证出△BAD≌△CAE即可；
（2）根据全等推出∠DBA=∠C，根据等腰三角形性质得出∠C=∠ABC，根据平行线性质得出∠ABC=∠DFB，推出∠DFB=∠DBF，根据等腰三角形的判定推出即可．
（1）∵∠BAC=∠DAE，∴∠BAC﹣∠BAE=∠DAE﹣∠BAE，∴∠BAD=∠EAC．在△BAD和△CAE中，∵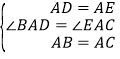
，∴△BAD≌△CAE（SAS）；
（2）∵△BAD≌△CAE，∴∠DBA=∠C．
∵AB=AC，∴∠C=∠ABC．
∵DF∥BC，∴∠DFB=∠ABC=∠C=∠DBA，即∠DFB=∠DBF，∴DF=CE．
名师点睛字词句段篇系列答案科目：初中数学 来源： 题型：
【题目】甲正在阅读《三国演义》，每天所读页数相同，当他读完第84页时，乙从头开始阅读同一本书籍，每天所读页数相同；下列表格记录了甲乙两人同读《三国演义》的进度．例如：第五天结束时，两人已读页数之和为424，此时甲比乙多读了24页；（注：已读页数中已计入了甲先读完的84页）
同读天数 | 1 | 2 | 3 | 4 | 5 |
已读页数之和 | 152 | 220 | a | b | 424 |
已读页数之差 | 72 | 60 | 48 | 36 | 24 |
（1）请直接写出表格中a、b的值；
（2）列方程求解：甲、乙两人每天各读书多少页？
（3）若这本书共有520页，从第6天起，甲每天比原来多读n页，乙每天所读页数不变，这样到第11天结束时，甲、乙两人已读页数相同，求n的值．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】小美周末来到公园，发现在公园一角有一种“守株待兔”游戏．游戏设计者提供了一只兔子和一个有A、B、C、D、E五个出入口的兔笼，而且笼内的兔子从每个出入口走出兔笼的机会是均等的．规定：
①玩家只能将小兔从A、B两个出入口放入；
②如果小兔进入笼子后选择从开始进入的出入口离开，则可获得一只价值5元小兔玩具，否则应付费3元．
（1）问小美得到小兔玩具的机会有多大？
（2）假设有100人次玩此游戏，估计游戏设计者可赚多少元？
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图，在半径为R的⊙O中，
和
度数分别为36°和108°，弦CD与弦AB长度的差为（用含有R的代数式表示）．
A. R B. 
C. 2R D. 3R
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】“绿水青山就是金山银山”，为保护生态环境，某地准备开荒种树，两次参加活动的人数及开支如下表：
开荒（人） | 种树（人） | 总支出（元） | |
第一次 | 15 | 9 | 57000 |
第二次 | 10 | 16 | 68000 |
（1）若两次开荒种树活动的人均支出费用一样，求开荒和种树的人均支出费用各是多少？
（2）在人均支出费用不变的情况下，为节约开支，施工单位准备抽调40人参加此活动，要使得总支出不超过102 000元，且开荒人数小于种树人数，则有哪几种分配人员方案？
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图，在
中，
是
边上的一点，
是
的中点，过点
作的平行线交
的延长线于
，且
，连结
．
（1）求证：是的中点；
（2）如果
，试猜测四边形
的形状，并证明你的结论．
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com
