

|
|
| 1 |
| 2 |
| 1 |
| 2 |

| OE |
| OH |
| ON |
| OM |
| 3 |
| 2 |
| y |
| x |
| 3 |
| 2 |


科目:初中数学 来源: 题型:
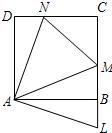 20、如图,正方形ABCD的边长为1,点M、N分别在BC、CD上,使得△CMN的周长为2,将△AND绕点A顺时针旋转90°得△ABL,求证:△ANM≌△ALM.
20、如图,正方形ABCD的边长为1,点M、N分别在BC、CD上,使得△CMN的周长为2,将△AND绕点A顺时针旋转90°得△ABL,求证:△ANM≌△ALM.查看答案和解析>>
科目:初中数学 来源: 题型:
| 3 |
查看答案和解析>>
科目:初中数学 来源: 题型:
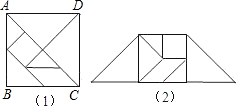 七巧板是我们祖先创造的一种智力玩具,它来源于勾股法,如图(1)整幅七巧板是由正方形ABCD分割成大小七块(其中五块是等腰三角形,一块是正方形和一块平行四边形)组成,如图(2)是由七巧板拼成一个梯形,如果正方形ABCD的边长为2
七巧板是我们祖先创造的一种智力玩具,它来源于勾股法,如图(1)整幅七巧板是由正方形ABCD分割成大小七块(其中五块是等腰三角形,一块是正方形和一块平行四边形)组成,如图(2)是由七巧板拼成一个梯形,如果正方形ABCD的边长为2| 2 |
| A、8 | ||
B、8+4
| ||
C、8
| ||
| D、16 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com