
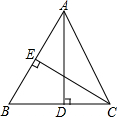
 如图,AD,CE是△ABC的高,已知AD=10,CE=9,AB=12,则BC=
如图,AD,CE是△ABC的高,已知AD=10,CE=9,AB=12,则BC=科目:初中数学 来源: 题型:
| 码号 | 33 | 34 | 35 | 36 | 37 |
| 人数 | 7 | 6 | 15 | 1 | 1 |
| A、平均数 | B、中位数 |
| C、众数 | D、无法确定 |
查看答案和解析>>
科目:初中数学 来源: 题型:
 如图,AB是半圆O的直径,点C、D、E是半圆弧上的点,且弦AC=CD=2,弦DE=EB=
如图,AB是半圆O的直径,点C、D、E是半圆弧上的点,且弦AC=CD=2,弦DE=EB=| 2 |
A、2
| ||
B、2
| ||
C、3
| ||
D、4
|
查看答案和解析>>
科目:初中数学 来源: 题型:
查看答案和解析>>
科目:初中数学 来源: 题型:
| A、对称轴是直线x=1 |
| B、顶点坐标是(1,2) |
| C、当x>1时,y随x的增大而减小 |
| D、当x=1时,函数y的最小值为2 |
查看答案和解析>>
科目:初中数学 来源: 题型:
 芳芳用水管以均匀的速度向一个容器中注水,在注水过程中,水面的高度h与注水时间t之间的函数图象如图所示,最后芳芳将容器注满水,则这个容器的形状大致为( )
芳芳用水管以均匀的速度向一个容器中注水,在注水过程中,水面的高度h与注水时间t之间的函数图象如图所示,最后芳芳将容器注满水,则这个容器的形状大致为( )A、 |
B、 |
C、 |
D、 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com