
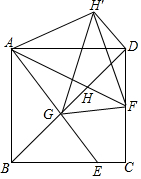
 如图,正方形ABCD的边长为4,点E是BC上的一点,连接AE,AF平分∠DAE交DC于点F,连接BD分别交AE,AF于点G,H,将△ADH沿直线AD翻折,点H落在点H′处,连接GH′,H′F,FG,若DF=FC,则△H′GF的面积是4.
如图,正方形ABCD的边长为4,点E是BC上的一点,连接AE,AF平分∠DAE交DC于点F,连接BD分别交AE,AF于点G,H,将△ADH沿直线AD翻折,点H落在点H′处,连接GH′,H′F,FG,若DF=FC,则△H′GF的面积是4. 分析 如图,作辅助线,构建直角三角形,利用S△H′GF=S梯形H′GQP-S△H′PF-S△GQF求出面积;根据勾股定理列方程先求EC=1,由平行线得三角形相似列比例式分别求GQ、PQ、H'P的长,代入最后可得结论.
解答 解:如图,∵DF=FC,DC=4,
∴DF=FC=2,
∵四边形ABCD是正方形,
∴∠ADC=∠BAD=90°,
在Rt△ADF中,AD=4,
∴AF=$\sqrt{{4}^{2}+{2}^{2}}$=2$\sqrt{5}$,
同理可得:BD=4$\sqrt{2}$,
∵AB∥DF,
∴△ABH∽△FDH,
∴$\frac{BH}{DH}$=$\frac{AB}{DF}=\frac{4}{2}$=2,
∴DH=$\frac{4\sqrt{2}}{3}$,
由折叠得:DH′=DH=$\frac{4\sqrt{2}}{3}$,∠ADH′=∠ADH=45°,
过H′作H′P⊥CD,交CD的延长线于P,过G作GQ⊥CD于Q,
∴∠HDP=45°,
∴H′P=PD=$\frac{4}{3}$,
连接EF,过F作FK⊥AE于K,
∵AF平分∠EAD,
∴DF=FK=2,
∴FK=FC=2,
∵EF=EF,
∴Rt△FEK≌Rt△FEC(HL),
∴EK=EC,
易得△ADF≌△AKF,
∴AD=AK=4,
设EC=x,则BE=4-x,AE=4+x,
在Rt△ABE中,由勾股定理得:42+(4-x)2=(4+x)2,
x=1,
∴BE=3,EC=1,
∵AD∥BC,
∴△AGD∽△EGB,
∴$\frac{DG}{BG}$=$\frac{AD}{BE}$=$\frac{4}{3}$,
∴$\frac{DG}{DB}=\frac{4}{7}$,
∵GQ∥BC,
∴△DGQ∽△DBC,
∴$\frac{GQ}{BC}$=$\frac{DQ}{DC}$=$\frac{DG}{DB}$=$\frac{4}{7}$,
∴$\frac{GQ}{4}$=$\frac{4}{7}$=$\frac{DQ}{4}$,
∴GQ=DQ=$\frac{16}{7}$,
∴FQ=DQ-DF=$\frac{16}{7}$-2=$\frac{2}{7}$,
∴S△H′GF=S梯形H′GQP-S△H′PF-S△GQF,
=$\frac{1}{2}$($\frac{4}{3}$+$\frac{16}{7}$)($\frac{4}{3}$+$\frac{16}{7}$)-$\frac{1}{2}$×$\frac{4}{3}$×$(\frac{4}{3}+2)$-$\frac{1}{2}×\frac{2}{7}×\frac{16}{7}$,
=4.
故答案为:4.
点评 本题考查了正方形的性质、翻折变换的性质、三角形全等和相似的性质和判定、勾股定理、角平分线的性质等知识,有难度,作辅助线证明EC=1是关键.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:选择题
| A. | 1 | B. | $\frac{1}{3}$ | C. | 3 | D. | -1 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
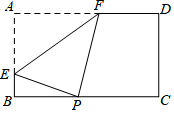 如图,矩形纸片ABCD中,AB=6,AD=10,P是边BC上的动点,现将纸片折叠,使点A与点P重合,折痕与矩形边的交点分别是E,F,要使折痕始终与边AB,AD有交点,则BP的取值范围是( )
如图,矩形纸片ABCD中,AB=6,AD=10,P是边BC上的动点,现将纸片折叠,使点A与点P重合,折痕与矩形边的交点分别是E,F,要使折痕始终与边AB,AD有交点,则BP的取值范围是( )| A. | $\sqrt{5}≤BP≤5$ | B. | 2≤BP≤6 | C. | $\sqrt{5}≤BP≤6$ | D. | $2≤BP≤5\sqrt{3}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
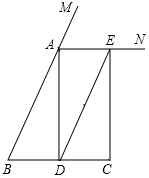 已知:如图,在△ABC中,AB=AC,AD是△ABC的中线,AN为△ABC的外角∠CAM的平分线,CE∥AD,交AN于点E.求证:四边形ADCE是矩形.
已知:如图,在△ABC中,AB=AC,AD是△ABC的中线,AN为△ABC的外角∠CAM的平分线,CE∥AD,交AN于点E.求证:四边形ADCE是矩形.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | $\frac{x-y}{x+y}$=-$\frac{y-x}{y+x}$ | B. | $\frac{-a-b}{a+b}$=-1 | C. | $\sqrt{{(1-\sqrt{2})}^{2}}$=$\sqrt{2}$-1 | D. | $\sqrt{{a}^{2}}$=a |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com