
 如图,已知DE∥BC,EF∥CD,且E在边AC上,F、D在边AB上,若AE:CE=2:1,DF=2,求AF、BD的长.
如图,已知DE∥BC,EF∥CD,且E在边AC上,F、D在边AB上,若AE:CE=2:1,DF=2,求AF、BD的长.  考前必练系列答案
考前必练系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
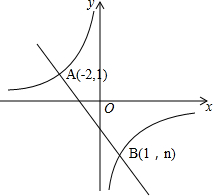 如图,一次函数y1=kx+b的图象与反比例函数y2=$\frac{m}{x}$的图象相交于A、B两点,
如图,一次函数y1=kx+b的图象与反比例函数y2=$\frac{m}{x}$的图象相交于A、B两点,查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 小惠同学学习了轴对你知识后,忽然想起了过去做过的一道题:有一组数排列成方阵,如图所示,试计算这组数的和,小惠想方阵就像小正方形,正方形是轴对称图形,能不能利用轴对称的思想来解决方阵的问题呢?小惠试了试,竟得到了非常巧妙的方法.请你试试看!
小惠同学学习了轴对你知识后,忽然想起了过去做过的一道题:有一组数排列成方阵,如图所示,试计算这组数的和,小惠想方阵就像小正方形,正方形是轴对称图形,能不能利用轴对称的思想来解决方阵的问题呢?小惠试了试,竟得到了非常巧妙的方法.请你试试看!查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com