
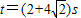 时,以点A为圆心,AP为半径的圆与以点B为圆心、BQ半径的圆的位置关系;除此之外⊙A与⊙B还有其他位置关系吗?如果有,请求出t的取值范围.
时,以点A为圆心,AP为半径的圆与以点B为圆心、BQ半径的圆的位置关系;除此之外⊙A与⊙B还有其他位置关系吗?如果有,请求出t的取值范围. 时AP,BQ的长即两圆的半径长,然后比较两圆的半径和圆心距即AB的距离即可判断出两圆的位置关系.
时AP,BQ的长即两圆的半径长,然后比较两圆的半径和圆心距即AB的距离即可判断出两圆的位置关系. ,
, ,∠AOP=∠BOQ=90度.
,∠AOP=∠BOQ=90度.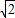 )s时,OP=2(2+4
)s时,OP=2(2+4 )-4=8
)-4=8 cm,
cm,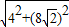 =12(cm),
=12(cm), ;
;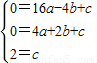

 x2-
x2- x+2.
x+2.

 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源:2003年全国中考数学试题汇编《二次函数》(05)(解析版) 题型:解答题
 时,以点A为圆心,AP为半径的圆与以点B为圆心、BQ半径的圆的位置关系;除此之外⊙A与⊙B还有其他位置关系吗?如果有,请求出t的取值范围.
时,以点A为圆心,AP为半径的圆与以点B为圆心、BQ半径的圆的位置关系;除此之外⊙A与⊙B还有其他位置关系吗?如果有,请求出t的取值范围.查看答案和解析>>
科目:初中数学 来源:2009年中考数学全真模拟试卷(9)(解析版) 题型:解答题
 时,以点A为圆心,AP为半径的圆与以点B为圆心、BQ半径的圆的位置关系;除此之外⊙A与⊙B还有其他位置关系吗?如果有,请求出t的取值范围.
时,以点A为圆心,AP为半径的圆与以点B为圆心、BQ半径的圆的位置关系;除此之外⊙A与⊙B还有其他位置关系吗?如果有,请求出t的取值范围.查看答案和解析>>
科目:初中数学 来源:2003年山东省滨州市中考数学试卷(解析版) 题型:解答题
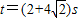 时,以点A为圆心,AP为半径的圆与以点B为圆心、BQ半径的圆的位置关系;除此之外⊙A与⊙B还有其他位置关系吗?如果有,请求出t的取值范围.
时,以点A为圆心,AP为半径的圆与以点B为圆心、BQ半径的圆的位置关系;除此之外⊙A与⊙B还有其他位置关系吗?如果有,请求出t的取值范围.查看答案和解析>>
科目:初中数学 来源:2003年全国中考数学试题汇编《数据收集与处理》(01)(解析版) 题型:选择题

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com