
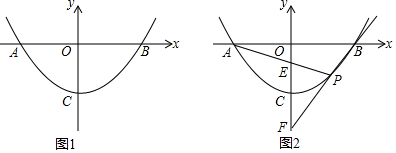
分析 (1)根据待定系数法求函数解析式,可得答案;根据平行线的判定,可得PD∥OB,根据函数值相等两点关于对称轴对称,可得D点坐标;
(2)根据待定系数法,可得E、F点的坐标,根据分式的性质,可得答案.
解答 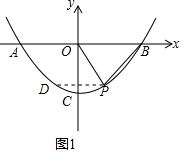 解:(1)将P(1,-3),B(4,0)代入y=ax2+c,得
解:(1)将P(1,-3),B(4,0)代入y=ax2+c,得
$\left\{\begin{array}{l}{16a+c=0}\\{a+c=-3}\end{array}\right.$,
解得$\left\{\begin{array}{l}{a=\frac{1}{5}}\\{c=-\frac{16}{5}}\end{array}\right.$,
抛物线的解析式为y=$\frac{1}{5}$x2-$\frac{16}{5}$.
∴C(0,-$\frac{16}{5}$)
如图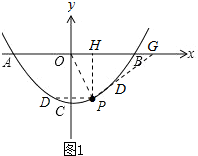 1,
1,
当点D在OP左侧时,
由∠DPO=∠POB,得
DP∥OB,
D与P关于y轴对称,P(1,-3),
得D(-1,-3);
(2)点P运动时,$\frac{OE+OF}{OC}$是定值,定值为2,理由如下:
作PQ⊥AB于Q点,设P(m,am2+c),A(-t,0),B(t,0),则at2+c=0,c=-at2.
∵PQ∥OF,
∴$\frac{PQ}{OF}$=$\frac{BQ}{BO}$,
∴OF=$\frac{PQ•BO}{BQ}$=-$\frac{-(a{m}^{2}+c)t}{t-m}$=$\frac{(a{m}^{2}-a{t}^{2})t}{m-t}$=amt+at2.
同理OE=-amt+at2.
∴OE+OF=2at2=-2c=2OC.
∴$\frac{OE+OF}{OC}$=2.
点评 本题考查了二次函数综合题,①利用待定系数法求函数解析式;②利用函数值相等的点关于对称轴对称得出D点坐标是解题关键;(2)利用待定系数法求出E、F点坐标是解题关键.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:选择题
| A. | 调查市场上某品牌老酸奶的质量情况 | |
| B. | 调查某品牌圆珠笔芯的使用寿命 | |
| C. | 调查乘坐飞机的旅客是否携带了危禁物品 | |
| D. | 调查我市市民对《徐州夜新闻》的认可情况 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 0 | B. | $\sqrt{2}$ | C. | -$\frac{1}{2}$ | D. | 0.3 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
 如图,已知直线AB、CD相交于点O,OE平分∠COB,若∠EOB=65°,则∠BOD的度数是( )
如图,已知直线AB、CD相交于点O,OE平分∠COB,若∠EOB=65°,则∠BOD的度数是( )| A. | 30° | B. | 40° | C. | 50° | D. | 60° |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | (x+2)(x-3) | B. | (x+6)(x-1) | C. | (x-2)(x+3) | D. | (x-6)(x+1) |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
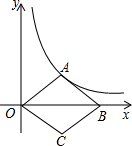 如图,在平面直角坐标系中,点O为原点,菱形OABC的对角线OB在x轴上,顶点A在反比例函数y=$\frac{3}{x}$的图象上,则菱形的面积为( )
如图,在平面直角坐标系中,点O为原点,菱形OABC的对角线OB在x轴上,顶点A在反比例函数y=$\frac{3}{x}$的图象上,则菱形的面积为( )| A. | 6 | B. | 5 | C. | 4 | D. | 3 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | (ab)2=ab2 | B. | a2•a3=a6 | C. | (-$\sqrt{2}$)2=4 | D. | $\sqrt{2}$×$\sqrt{3}$=$\sqrt{6}$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com