
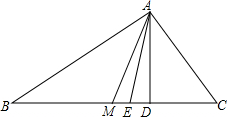
 已知:如图,在△ABC中,AB>AC,AM是中线,AD是高,AE是角平分线,并且∠DAE=∠MAE,求证:∠BAC=90°.
已知:如图,在△ABC中,AB>AC,AM是中线,AD是高,AE是角平分线,并且∠DAE=∠MAE,求证:∠BAC=90°. 分析 作△ABC的外接圆,延长AM,AE,AD,交其外接圆于M′,E′,D′,连接BD′,D′E′,E′M′,M′C,D′M′,由AE是角平分线,并且∠DAE=∠MAE,得到∠BAE=∠CA推出$\widehat{BM′}$=$\widehat{CD′}$,于是得到$\widehat{BD′}$=$\widehat{CM′}$,M′D′∥BC,求得BD′=CM′,证得AM′是圆的直径,得到∠AE′M′=90°,得到ME′⊥BC,推出ME′∥AD,于是得到∠ME′A=∠EAD=∠MAE,得到AM=ME′,由于∠M′E′M=90°-∠ME′A=90°-∠MAE′=∠MM′E′,于是得到MM′=ME′=AM,即点M是圆心,求得BC是直径,即可得到结论.
解答 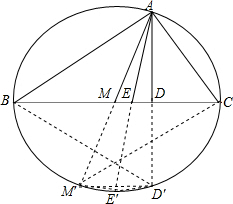 解:作△ABC的外接圆,延长AM,AE,AD,交其外接圆于M′,E′,D′,连接BD′,D′E′,E′M′,M′C,D′M′,
解:作△ABC的外接圆,延长AM,AE,AD,交其外接圆于M′,E′,D′,连接BD′,D′E′,E′M′,M′C,D′M′,
∵AE是角平分线,并且∠DAE=∠MAE,
∴∠BAE=∠CAE,
∴∠BAM=∠CAD,
∴$\widehat{BM′}$=$\widehat{CD′}$,
∴$\widehat{BD′}$=$\widehat{CM′}$,M′D′∥BC,
∴BD′=CM′,
∴D′E′=E′M′,
∵AD⊥BC,
∴D′M′⊥AD′,
∴AM′是圆的直径,
∴∠AE′M′=90°,
∵AM是AM是中线,E′是$\widehat{BC}$的中点,
∴ME′⊥BC,
∴ME′∥AD,
∴∠ME′A=∠EAD=∠MAE,
∴AM=ME′,∵∠M′E′M=90°-∠ME′A=90°-∠MAE′=∠MM′E′,
∴MM′=ME′=AM,
即点M是圆心,∴BC是直径,
∴∠BAC=90°.
点评 本题考查了三角形的内角和,垂径定理,圆周角定理,正确的作出辅助线是解题的关键.


 备战中考寒假系列答案
备战中考寒假系列答案科目:初中数学 来源: 题型:解答题

查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 某居民小区一处圆柱形的输水管道破裂,维修人员为更换管道,需确定管道圆形截面的半径,下图是水平放置的破裂管道有水部分的截面.
某居民小区一处圆柱形的输水管道破裂,维修人员为更换管道,需确定管道圆形截面的半径,下图是水平放置的破裂管道有水部分的截面.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com