
【题目】在正方形网格中,每个小正方形的边长均为1个单位长度,△ABC的三个顶点的位置如图所示.现将△ABC平移,使点A变换为点D,点E、F分别是B、C的对应点.
(1)请画出平移后的△DEF;
(2)若连接AD、CF,则这两条线段之间的关系是________________;
(3)在图中找出所有满足S△ABC=S△QBC的格点Q (异于点A),并用Q1、Q2…表示.

科目:初中数学 来源: 题型:
【题目】如图,每个小正方形的边长为1,在方格纸内将![]() 经过一次平移后得到
经过一次平移后得到![]() ,图中标出了点B的对应点
,图中标出了点B的对应点![]() .根据下列条件,利用网格点和直尺画图:
.根据下列条件,利用网格点和直尺画图:
(1)补全![]() ;
;
(2)作出中线![]() ;
;
(3)画出![]() 边上的高线
边上的高线![]() ;
;
(4)在平移过程中,线段![]() 扫过的面积为 .
扫过的面积为 .

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一副三角板如图1摆放,∠C=∠DFE=90,∠B=30,∠E=45,点F在BC上,点A在DF上,且AF平分∠CAB,现将三角板DFE绕点F顺时针旋转(当点D落在射线FB上时停止旋转).
(1)当∠AFD=_ __时,DF∥AC;当∠AFD=__ _时,DF⊥AB;
(2)在旋转过程中,DF与AB的交点记为P,如图2,若AFP有两个内角相等,求∠APD的度数;
(3)当边DE与边AB、BC分别交于点M、N时,如图3,若∠AFM=2∠BMN,比较∠FMN与∠FNM的大小,并说明理由。

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】观察下列等式:
12×231=132×21,
13×341=143×31,
23×352=253×32,
34×473=374×43,
62×286=682×26,
……
以上每个等式中两边数字是分别对称的,且每个等式中组成两位数与三位数的数字之间具有相同规律,我们称这类等式为“数字对称等式”.
(1)根据上述各式反映的规律填空,使式子成为“数字对称等式”:
①52× = ×25;
② ×396=693× .
(2)设这类等式左边两位数的十位数字为![]() ,个位数字为
,个位数字为![]() ,且2≤
,且2≤![]() ≤9,写出表示“数字对称等式”一般规律的式子(含
≤9,写出表示“数字对称等式”一般规律的式子(含![]() 、
、![]() ),并说明理由.
),并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一个直角三角形的两条直角边分别为![]() 、
、![]()
![]() ,斜边为
,斜边为![]() .我国古代数学家赵爽用四个这样的直角三角形拼成了如图的正方形,
.我国古代数学家赵爽用四个这样的直角三角形拼成了如图的正方形,
(1)探究活动:如图1,中间围成的小正方形的边长为 (用含有![]() 、
、![]() 的代数式表示);
的代数式表示);
(2)探究活动:如图1,用不同的方法表示这个大正方形的面积,并写出你发现的结论;

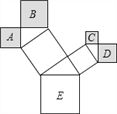
图1 图2
(3)新知运用:根据你所发现的结论完成下列问题.
①某个直角三角形的两条直角边![]() 、
、![]() 满足式子
满足式子![]() ,求它的斜边
,求它的斜边![]() 的值;
的值;
②由①中结论,此三角形斜边![]() 上的高为 .
上的高为 .
③如图2,这个勾股树图形是由正方形和直角三角形组成的,若正方形![]() 、
、![]() 、
、![]() 、
、![]() 的面积分别为
的面积分别为![]() ,4,
,4, ![]() ,
, ![]() .则最大的正方形
.则最大的正方形![]() 的边长是 .
的边长是 .
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com