
【题目】已知直线y=kx+1经过点M(d,﹣2)和点N(1,2),交y轴于点H,交x轴于点F.
(1)求d的值;
(2)将直线MN绕点M顺时针旋转45°得到直线ME,点Q(3,e)在直线ME上,①证明ME∥x轴;②试求过M、N、Q三点的抛物线的解析式;
(3)在(2)的条件下,连接NQ,作△NMQ的高NB,点A为MN上的一个动点,若BA将△NMQ的面积分为1:2两部分,且射线BA交过M、N、Q三点的抛物线于点C,试求点C的坐标.

【答案】(1)d=﹣3;
(2)①证明见解析,
②y=﹣![]() x2+
x2+![]() ;
;
(3)点C的坐标为(1﹣2![]() ,2
,2![]() ﹣2)和(1,2).
﹣2)和(1,2).
【解析】
试题分析:(1)把点N(1,2)代入y=kx+1,得k,再把M点坐标代入已知直线解析式得d;
(2)由(1)可知直线MN:y=x+1与x轴夹角为45°,将直线MN绕点M顺时针旋转45°得到直线ME,此时ME∥x轴;由此可以判断点Q的纵坐标与点M相同,e=﹣2,已知M、N、Q三点坐标,可求抛物线解析式;
(3)有两种可能,即S△AMB=![]() S△NMQ或S△AMB=
S△NMQ或S△AMB=![]() S△NMQ;△NMQ的面积为已知,线段MB长已知,可求点A到BM的距离,又点A在直线MN上,可求点A坐标,用“两点法”求直线AB解析式,再与抛物线解析式联立,可求C点坐标.
S△NMQ;△NMQ的面积为已知,线段MB长已知,可求点A到BM的距离,又点A在直线MN上,可求点A坐标,用“两点法”求直线AB解析式,再与抛物线解析式联立,可求C点坐标.
试题解析:(1)把点N(1,2)代入y=kx+1,得k=1
∴y=x+1
∵点M(d,﹣2)在直线y=x+1上
∴d=﹣3
(2)①∵y=x+1分别交x轴、y轴于点F、H.
∴F(﹣1,0),H(0,1),
∴OF=OH=1
∴∠HFO=∠NME=45°,
∴ME∥x轴
②又∵点Q(3,e)在直线ME上,
∴Q(3,﹣2)
设过M(﹣3,﹣2),N(1,2),Q(3,﹣2)的抛物线为y=ax2+bx+c
代入三个点的坐标得
解得
∴y=﹣![]() x2+
x2+![]()
(3)设A(m,n),A到MQ的距离为h,则
S△AMB=![]() S△NMQ或S△AMB=
S△NMQ或S△AMB=![]() S△NMQ
S△NMQ
当S△AMB=![]() S△NMQ时,得
S△NMQ时,得![]() MBh=
MBh=![]() ×
×![]() MQNB ①
MQNB ①
∵NB是△NMQ的高,
∴B(1,﹣2)
∴MB=4,MQ=6,NB=4
∴由①式得h=2,
∴n=2﹣2=0,m=﹣1
∴A(﹣1,0)
设直线AB的解析式为y=kx+b,代入A(﹣1,0)和B(1,﹣2),得k=﹣1,b=﹣1
解方程组
得
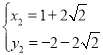 (舍去)
(舍去)
∴C(1﹣2![]() ,2
,2![]() ﹣2)
﹣2)
当S△AMB=![]() S△NMQ时,可得h=4,n=2,m=1
S△NMQ时,可得h=4,n=2,m=1
此时点A(1,2)为满足条件的点
综上可知,所求点C的坐标为(1﹣2![]() ,2
,2![]() ﹣2)和(1,2).
﹣2)和(1,2).


科目:初中数学 来源: 题型:
【题目】张老师带领x名学生到某动物园参观,已知成人票每张10元,学生票每张5元,设门票的总费用为y元,则y=__________________,当学生有45人时,需要的总费用为________元.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】鄂州市化工材料经销公司购进一种化工原料若干千克,价格为每千克30元.物价部门规定其销售单价不高于每千克60元,不低于每千克30元.经市场调查发现:日销售量y(千克)是销售单价x(元)的一次函数,且当x=60时,y=80;x=50时,y=100.在销售过程中,每天还要支付其他费用450元.
(1)求出y与x的函数关系式,并写出自变量x的取值范围.
(2)求该公司销售该原料日获利w(元)与销售单价x(元)之间的函数关系式.
(3)当销售单价为多少元时,该公司日获利最大?最大获利是多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】两个小组进行定点投篮对抗赛,每组6名组员,每人投10次.两组组员进球数的统计结果如下:
组别 | 6名组员的进球数 | 平均数 | |||||
甲组 | 8 | 5 | 3 | 1 | 1 | 0 | 3 |
乙组 | 5 | 4 | 3 | 3 | 2 | 1 | 3 |
则组员投篮水平较整齐的小组是____组.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】数轴上表示整数的点称为整点。某数轴的单位长度是1厘米,若在这个数轴上随意画出一条长为2004厘米的线段AB,则线段AB盖住的整点的个数是( )
A.2002或2003
B.2003或2004
C.2004或2005
D.2005或2006
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com