
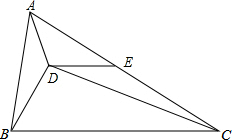
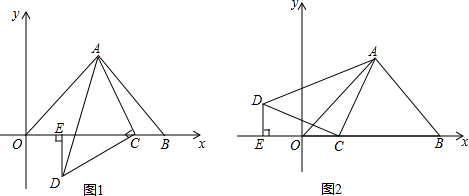
 已知D是△ABC内一点,E是边AC的中点,AB=6,BC=10,∠BAD=∠BCD,∠EDC=∠ABD.求DE的长.
已知D是△ABC内一点,E是边AC的中点,AB=6,BC=10,∠BAD=∠BCD,∠EDC=∠ABD.求DE的长. 分析 延长CD到F、使CD=DF知DE∥AF、DE=$\frac{1}{2}$AF,通过∠ABD=∠DFA=∠EDC知点A、F、B、D四点共圆,从而得到∠BFD=∠BCD=∠BAD,证△BFD≌△BCD知∠BAF=∠BDF=90°,在RT△BAF中根据勾股定理可得AF的长即可.
解答 解:如图,延长CD到F,使CD=DF,连接AF、BF,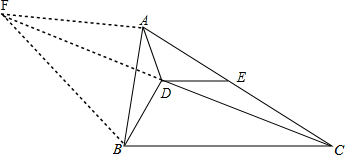
∵E是AC中点,CD=DF,
∴DE∥AF,且DE=$\frac{1}{2}$AF,
∴∠CDE=∠DFA,
∵∠EDC=∠ABD,
∴∠ABD=∠DFA=∠EDC,
∴点A、F、B、D四点共圆,
∴∠BAD=∠BFD,
又∵∠BAD=∠BCD,
∴∠BFD=∠BCD,
∴BF=BC,
在△BFD和△BCD中,
∵$\left\{\begin{array}{l}{BF=BC}\\{BD=BD}\\{DC=DF}\end{array}\right.$,
∴△BFD≌△BCD(SSS),
∴∠BDF=∠BDC=$\frac{1}{2}$∠CDF=90°,
∵点A、F、B、D四点共圆,
∴∠BAF=∠BDF=90°,
在RT△BAF中,∵BF=BC=10,AB=6,
∴AF=8,
∴DE=$\frac{1}{2}$AF=4.
点评 本题主要考查全等三角形的判定和性质,添加辅助线构造△BFD≌△BCD是解题的关键.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源:2017届江苏省徐州市九年级下学期第一次(3月)月考数学试卷(解析版) 题型:判断题
购买6件A商品和5件B商品共需270元,购买3件A商品和4件B商品共需180元.问:购买1件A商品和1件B商品共需多少元?
查看答案和解析>>
科目:初中数学 来源:2016-2017学年江西省新余市八年级下学期第一次段考数学试卷(解析版) 题型:单选题
如图所示:数轴上点A所表示的数为a,则a的值是( )
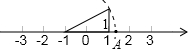
A. 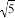 +1 B. -
+1 B. -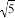 +1 C.
+1 C. 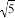 -1 D.
-1 D. 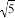
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题

查看答案和解析>>
科目:初中数学 来源: 题型:选择题
 已知:如图,∠1=∠2.
已知:如图,∠1=∠2.| A. | ③④ | B. | ④⑤ | C. | ⑤④ | D. | ⑤② |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com