
 ∥AB,F是
∥AB,F是 上的一点,且AB=AF,则点F到直线BC的距离为__________
上的一点,且AB=AF,则点F到直线BC的距离为__________
 ,又AB=AF;所以,在直角△AEF中,可运用勾股定理求得DF的长即为点F到BC的距离.
,又AB=AF;所以,在直角△AEF中,可运用勾股定理求得DF的长即为点F到BC的距离.
 =
= ,
, ;
; )2,
)2, ;
;
 )2,
)2, 故答案为:
故答案为: .
.

科目:初中数学 来源:不详 题型:解答题
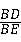 =
=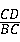 ;
;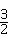 AB,求tan∠CDF的值.
AB,求tan∠CDF的值.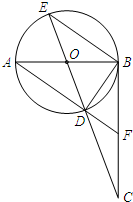
查看答案和解析>>
科目:初中数学 来源:不详 题型:填空题
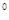 和 10
和 10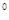 ,大灯A与地面离地面的距离为lm则该车大灯照亮地面的宽度BC是 m .(不考虑其它因素)
,大灯A与地面离地面的距离为lm则该车大灯照亮地面的宽度BC是 m .(不考虑其它因素)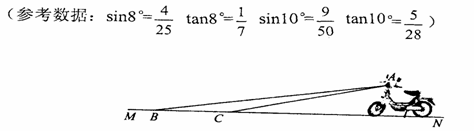
查看答案和解析>>
科目:初中数学 来源:不详 题型:解答题

查看答案和解析>>
科目:初中数学 来源:不详 题型:单选题

| A.8tan20° | B. | C.8sin20° | D.8cos20° |
查看答案和解析>>
科目:初中数学 来源:不详 题型:单选题
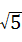 ,BC=2,则sin∠ACD的值为( )
,BC=2,则sin∠ACD的值为( )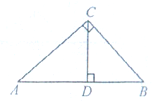
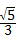 B、
B、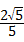
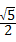 D、
D、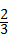
查看答案和解析>>
科目:初中数学 来源:不详 题型:解答题

 ,AE=
,AE= ,
,查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com