
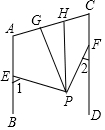
 如图:AB∥CD,PG平分∠EPF,PH∥CD,下列结论:
如图:AB∥CD,PG平分∠EPF,PH∥CD,下列结论:| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
分析 根据AB∥CD,PH∥CD,可得AB∥CD∥PH,再根据平行线的性质以及角的和差关系进行计算,即可得出正确结论.
解答 解:∵AB∥CD,PH∥CD,
∴AB∥CD∥PH,
∴∠1=∠EPH,∠2=∠FPH,
∴∠1+∠2=∠EPF,
又∵PG平分∠EPF,
∴∠EPF=2∠EPG,故①正确;
∵∠2=∠FPH,∠EPG=∠FPG,
∴∠EPG-∠GPH=∠FPG-∠GPH=∠FPH=∠2,故②正确;
∵∠GPH与∠FPH不一定相等,
∴∠FPH=∠GPH不一定成立,故③错误;
∵∠1-∠2=∠EPH-∠FPH=(EPG+∠GPH)-∠FPH=∠FPG+∠GPH-∠FPH=∠GPH+∠GPH=2∠GPH,
∴$\frac{∠1-∠2}{∠GPH}$=2,为定值,故④正确.
故选:C.
点评 本题主要考查了平行线的性质以及角平分线的定义的运用,解题时注意:两直线平行,内错角相等.


科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
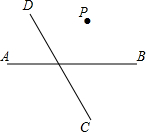 读句画图,如图直线AB与直线CD相交于C
读句画图,如图直线AB与直线CD相交于C查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | $\left\{\begin{array}{l}{x+y=0}\\{x-y=2}\end{array}\right.$ | B. | $\left\{\begin{array}{l}{x+y=0}\\{x-y=-2}\end{array}\right.$ | C. | $\left\{\begin{array}{l}{x+y=0}\\{x-y=4}\end{array}\right.$ | D. | $\left\{\begin{array}{l}{x+y=0}\\{x-y=-4}\end{array}\right.$ |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com