
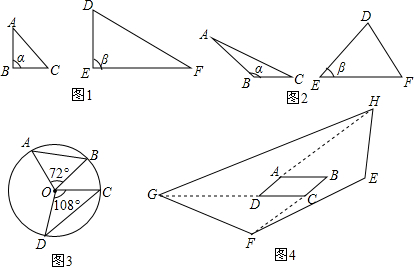
分析 (1)①②根据共角三角形的定义,可得答案;
(2)根据同角的补角相等,可得:∠ABM=∠E,根据相似三角形的判定,可得△ABM∽△DEN,根据相似三角形的性质,可得对应边的比相等,可得证明的结论;
(3)根据共角三角形面积的关系,可得答案;
(4)根据共角三角形面积的关系,可得共角三角形的面积,根据面积的和差,可得答案..
解答 解:(1)根据共角三角形的定义可知①对 ②错;
故答案为对,错.
(2)③证明:如图2中,过A作AM⊥BC交BC的延长线于点M、过D作DN⊥EF于点N,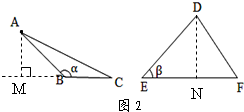
∴∠AMB=∠DNE=90°
又∵∠ABM+α=β+α=180°
∴∠ABM=β
即:∠ABM=∠E
∴△ABM∽△DEN
∴$\frac{AM}{DN}$=$\frac{AB}{DE}$,
∴$\frac{{S}_{△ABC}}{{S}_{△DEF}}$=$\frac{\frac{1}{2}AM•BC}{\frac{1}{2}DN•EF}$=$\frac{AM}{DN}$•$\frac{BC}{EF}$=$\frac{AB}{DE}$•$\frac{BC}{EF}$=$\frac{AB•BC}{DE•EF}$;
(3)如图3中,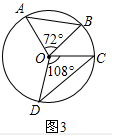
∵△OAB与△OCD是共角三角形,OA=OB=OC=OD,
∴$\frac{{S}_{△OAB}}{{S}_{△OCD}}$=$\frac{{S}_{1}}{{S}_{2}}$=$\frac{OA•OB}{OC•OD}$=1,
∴S1=S2;
故答案为:S1=S2.
(4)如图4中,连接AC、BD.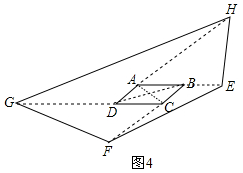
四边形ABCD的面积为2,
S△ABC=S△ADC=S△BAD=S△BCD=1,
使BE=AB,CF=2BC,DG=2CD,AH=3AD,
由共角三角形的面积比等于对应角两边的乘积之比得
$\frac{{S}_{△BEF}}{{S}_{△ABC}}$=$\frac{BE•EF}{AB•BC}$=$\frac{AB•3BC}{AB•BC}$=3,S△BEF=3,
$\frac{{S}_{△GCF}}{{S}_{△BCD}}$=$\frac{CG•CF}{CB•CD}$=$\frac{3CD•2BC}{CD•BC}$=6,S△GCF=6,
$\frac{{S}_{△HDG}}{{S}_{△ADC}}$=$\frac{DG•DH}{DA•DC}$=$\frac{2CD•4DA}{CD•DA}$=8,S△DGH=8,
$\frac{{S}_{△AHE}}{{S}_{△ADB}}$=$\frac{AH•AE}{AD•AB}$ $\frac{3AD•2AB}{AD•AB}$═6,S△AHE=6,
SEFGH=S△BEF+S△GCF+S△DGH+S△AHE+SABCD
=3+6+8+6+2=25,
故答案为25.
点评 本题考查了圆的综合题,共角三角形的面积之间的关系是解题关键.


科目:初中数学 来源: 题型:选择题
 如图,要设计一幅宽20cm,长30cm的图案,其中有两横两竖的彩条,横竖彩条的宽度比为2:1,如果要使彩条所占面积是图案面积的$\frac{19}{75}$,则竖彩条宽度为( )
如图,要设计一幅宽20cm,长30cm的图案,其中有两横两竖的彩条,横竖彩条的宽度比为2:1,如果要使彩条所占面积是图案面积的$\frac{19}{75}$,则竖彩条宽度为( )| A. | 1cm | B. | 1.5cm | C. | 2cm | D. | 2.5cm |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
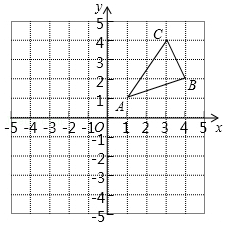 如图,△ABC三个顶点的坐标分别为A(1,1),B(4,2),C(3,4).
如图,△ABC三个顶点的坐标分别为A(1,1),B(4,2),C(3,4).查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com