
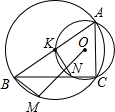
 ⊙O过△ABC顶点A,C,且与AB,BC交于K,N(K与N不同).△ABC外接圆和△BKN外接圆相交于B和M.求证:∠BMO=90°.(第26届IMO第五题)
⊙O过△ABC顶点A,C,且与AB,BC交于K,N(K与N不同).△ABC外接圆和△BKN外接圆相交于B和M.求证:∠BMO=90°.(第26届IMO第五题)  证明:连接OC,OK,MC,MK,延长BM到G,
证明:连接OC,OK,MC,MK,延长BM到G, |
| OC |
 |
| OK |


科目:初中数学 来源: 题型:
| DE | BE |
查看答案和解析>>
科目:初中数学 来源:中学学习一本通 数学 七年级下册 北师大课标 题型:044
如图所示,直线EF过△ABC顶点A,且EF∥BC,你能得到∠B+∠C+∠BAC的和是多少吗?说明理由.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com