
【题目】如图,![]() 的角平分线
的角平分线![]() ,
,![]() ,
,![]() 、
、![]() 所对的边记为
所对的边记为![]() 、
、![]() .
.
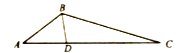
(1)当![]() 时,求
时,求![]() 的值;
的值;
(2)求![]() 的面积(用含
的面积(用含![]() ,
,![]() 的式子表示即可);
的式子表示即可);
(3)求证:![]() ,
,![]() 之和等于
之和等于![]() ,
,![]() 之积.
之积.
【答案】(1)2;(2)![]() ;(3)详见解析.
;(3)详见解析.
【解析】
(1)过点![]() 作
作![]() 于点
于点![]() ,利用直角三角形30度角的性质可知BE长,得
,利用直角三角形30度角的性质可知BE长,得![]() ,即点E、点D重合,中线与高线重合,可知AB=AC,即
,即点E、点D重合,中线与高线重合,可知AB=AC,即![]() ;
;
(2)表示方法有两种,可能情形1:过点![]() 作
作![]() 于点
于点![]() ,过点
,过点![]() 作
作![]() 延长线于点
延长线于点![]() ,解直角三角形可得
,解直角三角形可得![]() ,
,![]() ,利用三角形面积公式可得
,利用三角形面积公式可得
![]() 和
和![]() 的面积相加即可;可能情形2:过点
的面积相加即可;可能情形2:过点![]() 作
作![]() 于点
于点![]() ,解直角三角形可得
,解直角三角形可得![]() ,直接利用三角形面积公式求解即可;
,直接利用三角形面积公式求解即可;
(3)由(2)中面积的两种表示方法可直接证得结论.
解:(1)过点![]() 作
作![]() 于点
于点![]()
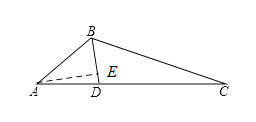
∵![]() 平分
平分![]() ,∴
,∴![]() .
.
在![]() 中,
中,![]() ,
,![]() .
.
∵![]() ,∴点
,∴点![]() 与点
与点![]() 重合,∴
重合,∴![]() .
.
∴![]() .
.
(2)答案不唯一.
可能情形1:过点![]() 作
作![]() 于点
于点![]() ,过点
,过点![]() 作
作![]() 延长线于点
延长线于点![]()
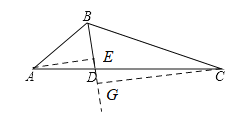
∵![]() 平分
平分![]() ,∴
,∴![]() .
.
∵在![]() 中,
中,![]() ,
,![]() ,
,
在![]() 中,
中,![]() ,
,![]()
∴![]()
![]() .
.
可能情形2:过点![]() 作
作![]() 于点
于点![]() ,用含
,用含![]() 的式子表示出
的式子表示出![]() ,
,
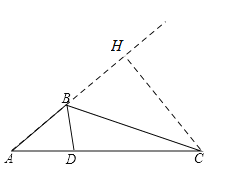
于是![]() .
.
(3)从上面![]() 两种面积表示方法
两种面积表示方法![]() ,
,![]() ,可得
,可得![]() ,化简得
,化简得![]() ,即
,即![]() ,
,![]() 之和等于
之和等于![]() ,
,![]() 之积.
之积.


 黄冈小状元解决问题天天练系列答案
黄冈小状元解决问题天天练系列答案 三点一测快乐周计划系列答案
三点一测快乐周计划系列答案科目:初中数学 来源: 题型:
【题目】如图,有一菱形纸片ABCD,∠A=60°,将该菱形纸片折叠,使点A恰好与CD的中点E重合,折痕为FG,点F、G分别在边AB、AD上,联结EF,那么cos∠EFB的值为____.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校开展了“文明城市”活动周,活动周设置了“![]() :文明礼仪,
:文明礼仪,![]() :生态环境,
:生态环境,![]() :交通安全,
:交通安全,![]() :卫生保洁”四个主题活动,每个学生限选一个主题参与,为了解活动开展情况,学校随机抽取了部分学生进行调查,并根据调查结果绘制了如下图所示的不完整的条形统计图和扇形统计图.
:卫生保洁”四个主题活动,每个学生限选一个主题参与,为了解活动开展情况,学校随机抽取了部分学生进行调查,并根据调查结果绘制了如下图所示的不完整的条形统计图和扇形统计图.
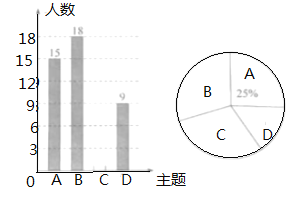
(1)本次随机调查的学生人数是_______人;
(2)补全条形统计图;
(3)在扇形统计图中,“![]() ”主题对应扇形的圆心角为________度.
”主题对应扇形的圆心角为________度.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,一次函数y=﹣x+5的图象与反比例函数![]() (k≠0)在第一象限的图象交于A(1,n)和B两点.
(k≠0)在第一象限的图象交于A(1,n)和B两点.

(1)求反比例函数的解析式及点B坐标;
(2)在第一象限内,当一次函数y=-x+5的值大于反比例函数![]() (k≠0)的值时,写出自变量x的取值范围.
(k≠0)的值时,写出自变量x的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在“母亲节”期间,某校部分团员参加社会公益活动,准备购进一批许愿瓶进行
销售,并将所得利润捐给慈善机构.根据市场调查,这种许愿瓶一段时间内的销售量y(个)于销售单价x(元
/个)之间的对应关系如图所示.
(1)试判断y与x之间的函数关系,并求出函数关系式;
(2)若许愿瓶的进价为6元/个,按照上述市场调查销售规律,求利润w(元)与销售单价x(元/个)之间的
函数关系式;
(3)若许愿瓶的进货成本不超过900元,要想获得最大利润,试求此时这种许愿瓶的销售单价,并求出
最大利润.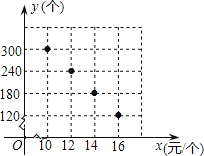
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在![]() 中,
中,![]() .以
.以![]() 为直径的
为直径的![]() 与
与![]() 交于点
交于点![]() ,与
,与![]() 交于点
交于点![]() ,点
,点![]() 在边
在边![]() 的延长线上,且
的延长线上,且![]() .
.
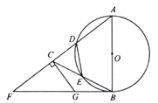
(1)试说明![]() 是
是![]() 的切线;
的切线;
(2)过点![]() 作
作![]() ,垂足为
,垂足为![]() .若
.若![]() ,
,![]() ,求
,求![]() 的半径;
的半径;
(3)连接![]() ,设
,设![]() 的面积为
的面积为![]() ,
,![]() 的面积为
的面积为![]() ,若
,若![]() ,
,![]() ,求
,求![]() 的长.
的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某体育用品商场预测某品牌运动服能够畅销,就用32000元购进了一批这种运动服,上市后很快脱销,商场又用68000元购进第二批这种运动服,所购数量是第一批购进数量的2倍,但每套进价多了10元.
(1)该商场两次共购进这种运动服多少套?
(2)如果这两批运动服每套的售价相同,且全部售完后总利润不低于20%,那么每套售价至少是多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某高科技产品开发公司现有员工50名,所有员工的月工资情况如下表:
员工 | 管理人员 | 普通工作人员 | |||||
人员结构 | 总经理 | 部门经理 | 科研人员 | 销售人员 | 高级技工 | 中级技工 | 勤杂工 |
员工数(名) | 1 | 3 | 2 | 3 | 24 | 1 | |
每人月工资(元) | 21000 | 8400 | 2025 | 2200 | 1800 | 1600 | 950 |
请你根据上述内容,解答下列问题:
(1)该公司“高级技工”有 名;
(2)所有员工月工资的平均数x为2500元,中位数为 元,众数为 元;
(3)小张到这家公司应聘普通工作人员.请你回答右图中小张的问题,并指出用(2)中的哪个数据向小张介绍员工的月工资实际水平更合理些;
(4)去掉四个管理人员的工资后,请你计算出其他员工的月平均工资![]() (结果保留整数),并判断
(结果保留整数),并判断![]() 能否反映该公司员工的月工资实际水平.
能否反映该公司员工的月工资实际水平.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知抛物线![]() 与x轴交于A、B两点(点A在点B的左侧),与y轴交于点C.
与x轴交于A、B两点(点A在点B的左侧),与y轴交于点C.
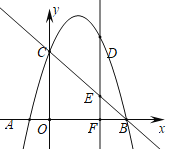
(1)直接写出点A、B、C的坐标;
(2)在抛物线的对称轴上存在一点P,使得PA+PC的值最小,求此时点P的坐标;
(3)点D是第一象限内抛物线上的一个动点(与点C、B不重合)过点D作DF⊥x轴于点F,交直线BC于点E,连接BD,直线BC把△BDF的面积分成两部分,使![]() ,请求出点D的坐标;
,请求出点D的坐标;
(4)若M为抛物线对称轴上一动点,使得△MBC为直角三角形,请直接写出点M的坐标.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com