
| A. | $\frac{x(x-1)}{2}$=2550 | B. | $\frac{x(x+1)}{2}$=2550 | C. | x(x-1)=2550 | D. | x(x+1)=2550 |
科目:初中数学 来源: 题型:选择题
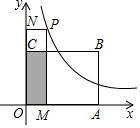 如图,矩形OABC的四个顶点分别为O(0,0),A(2,0),B(2,1),C(0,1),P(x,y)是反比例函数y=$\frac{1}{x}$(x>0)图象上的一个动点,过点P作PM⊥x轴,PN⊥y轴,M、N为垂足,记矩形OMPN与矩形OABC的重叠部分面积为S,则S与x轴的函数关系式的图象为( )
如图,矩形OABC的四个顶点分别为O(0,0),A(2,0),B(2,1),C(0,1),P(x,y)是反比例函数y=$\frac{1}{x}$(x>0)图象上的一个动点,过点P作PM⊥x轴,PN⊥y轴,M、N为垂足,记矩形OMPN与矩形OABC的重叠部分面积为S,则S与x轴的函数关系式的图象为( )| A. | 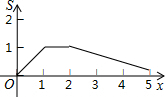 | B. | 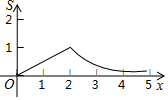 | ||
| C. | 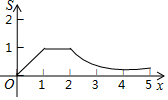 | D. | 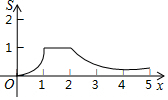 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
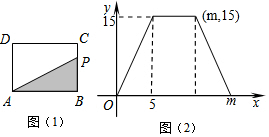
| A. | 6 | B. | 8 | C. | 11 | D. | 16 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题

查看答案和解析>>
科目:初中数学 来源: 题型:解答题
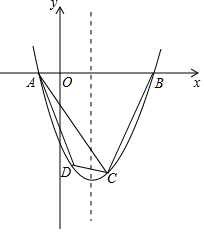 如图,在平面直角坐标系中,已知抛物线y=x2+bx+c经过A、B、C三点,已知B(4,0),C(2,-6).
如图,在平面直角坐标系中,已知抛物线y=x2+bx+c经过A、B、C三点,已知B(4,0),C(2,-6).查看答案和解析>>
科目:初中数学 来源: 题型:选择题
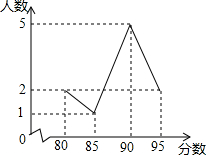 在学校演讲比赛中,10名选手的成绩折线统计图如图所示,则下列说法正确的是( )
在学校演讲比赛中,10名选手的成绩折线统计图如图所示,则下列说法正确的是( )| A. | 最高分90 | B. | 众数是5 | C. | 中位数是90 | D. | 平均分为87.5 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
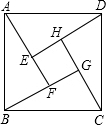 如图是我国汉代数学家赵爽在注解《周脾算经》时给出的“赵爽弦图”,图中的四个直角三角形是全等的,如果大正方形ABCD的面积是小正方形EFGH面积的13倍,那么tan∠ADE的值为( )
如图是我国汉代数学家赵爽在注解《周脾算经》时给出的“赵爽弦图”,图中的四个直角三角形是全等的,如果大正方形ABCD的面积是小正方形EFGH面积的13倍,那么tan∠ADE的值为( )| A. | $\frac{3}{2}$ | B. | $\frac{1}{2}$ | C. | $\frac{2}{3}$ | D. | $\frac{{2\sqrt{13}}}{13}$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com