
热气球的探测器显示,从热气球看一栋高楼顶部的仰角为30°,看这栋高楼底部的俯角为60°,热气球与高楼的水平距离为66 m,这栋高楼有多高(结果精确到0.1 m,参考数据:![]() ≈1.73)?
≈1.73)?
|
分析:把这个问题抽象成一个数学问题,在△ABC中,由已知可得∠B=60°,∠C=30°,过点A作AD⊥BC于点D,则AD=66 m,利用三角函数的有关知识,可以在 Rt△ABD和Rt△ACD中分别求出BD、CD的长,从而求出BC的长,即楼房的高度. 答:这栋楼高约为152.2 m. 解:如图,过点A作AD⊥BC,垂足为点D.
根据题意,可得∠BAD=30°,∠CAD=60°,AD=66. 在Rt△ADB中,由tan∠BAD= 得BD=AD·tan∠BAD=66×tan30°=66× 在Rt△ADC中,由tan∠CAD= 得CD=AD·tan∠CAD=66×tan60°=66 所以BC=BD+CD=22 点评:当一个三角形中出现30°、45°、60°角的时候,要求一些线段的长,通常是通过作高构造直角三角形,将这些特殊角放入直角三角形中,利用直角三角形边角关系求出线段的长. |


 中考解读考点精练系列答案
中考解读考点精练系列答案 各地期末复习特训卷系列答案
各地期末复习特训卷系列答案科目:初中数学 来源: 题型:
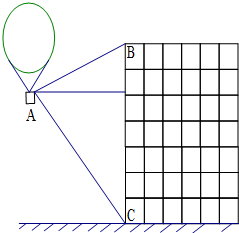 21、热气球的探测器显示,从热气球上看一栋高楼顶部的仰角为28°,看这栋高楼底部的俯角为62°,热气球与高楼之间的水平距离为66m,这栋高楼有多高?(结果精确到0.1m,参考数据:sin28°≈0.47,cos28°≈0.88,tan28°≈0.53,sin62°≈0.88,cos62°≈0.47,tan62°≈1.88)
21、热气球的探测器显示,从热气球上看一栋高楼顶部的仰角为28°,看这栋高楼底部的俯角为62°,热气球与高楼之间的水平距离为66m,这栋高楼有多高?(结果精确到0.1m,参考数据:sin28°≈0.47,cos28°≈0.88,tan28°≈0.53,sin62°≈0.88,cos62°≈0.47,tan62°≈1.88)查看答案和解析>>
科目:初中数学 来源: 题型:
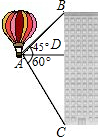 如图,热气球的探测器显示,从热气球看一栋高楼的顶部B的仰角为45°,看这栋高楼底部C的俯角为60°,热气球与高楼的水平距离AD为50m,求这栋楼的高度.(
如图,热气球的探测器显示,从热气球看一栋高楼的顶部B的仰角为45°,看这栋高楼底部C的俯角为60°,热气球与高楼的水平距离AD为50m,求这栋楼的高度.(| 2 |
| 3 |
查看答案和解析>>
科目:初中数学 来源: 题型:
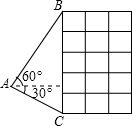 如图热气球的探测器显示,从热气球上看一栋高楼顶部的仰角为60°,看这栋高楼底部的俯角为30°,若热气球与高楼水平距离为60m,则这栋楼的高度为
如图热气球的探测器显示,从热气球上看一栋高楼顶部的仰角为60°,看这栋高楼底部的俯角为30°,若热气球与高楼水平距离为60m,则这栋楼的高度为| 3 |
| 3 |
查看答案和解析>>
科目:初中数学 来源: 题型:
 (2013•德阳)如图,热气球的探测器显示,从热气球A看一栋高楼顶部B的仰角为30°,看这栋高楼底部C的俯角为60°,热气球A与高楼的水平距离为120m,这栋高楼BC的高度为( )
(2013•德阳)如图,热气球的探测器显示,从热气球A看一栋高楼顶部B的仰角为30°,看这栋高楼底部C的俯角为60°,热气球A与高楼的水平距离为120m,这栋高楼BC的高度为( )查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com