
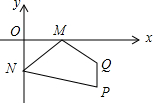
 如图,点P的坐标是(3,-2),点Q的坐标是(3,-1),点M是x轴上一个动点,点N是y轴上的一个动点,则四边形MNPQ周长的最小值是2$\sqrt{13}$+1.
如图,点P的坐标是(3,-2),点Q的坐标是(3,-1),点M是x轴上一个动点,点N是y轴上的一个动点,则四边形MNPQ周长的最小值是2$\sqrt{13}$+1. 分析 如图,作点P关于y轴的对称点P′,点Q关于y轴的对称点Q′,连接P′Q′交y轴于M,交x轴于N,此时四边形MNQP周长最小,根据PM+MN+NQ=P′M+MN+NQ′=P′Q′,利用勾股定理即可解决问题.
解答 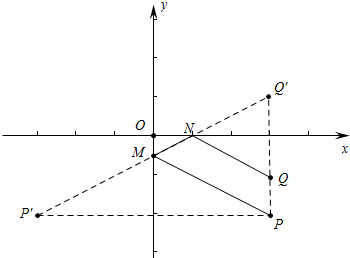 解:如图,作点P关于y轴的对称点P′,点Q关于y轴的对称点Q′,连接P′Q′交y轴于M,交x轴于N,
解:如图,作点P关于y轴的对称点P′,点Q关于y轴的对称点Q′,连接P′Q′交y轴于M,交x轴于N,
此时四边形MNQP周长最小,
∵PM+MN+NQ=P′M+MN+NQ′=P′Q′=$\sqrt{PP{′}^{2}+PQ{′}^{2}}$=$\sqrt{{6}^{2}+{4}^{2}}$=2$\sqrt{13}$,
∴四边形MNQP周长的最小值为2$\sqrt{13}$+1.
故答案为2$\sqrt{13}$+1
点评 本题考查轴对称-最短问题、坐标与图形的性质、勾股定理,线段垂直平分线性质等知识,解题的关键是利用轴对称正确找到点M、N的位置,利用勾股定理解决问题,属于中考常考题型.


科目:初中数学 来源: 题型:选择题
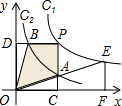 如图,两个反比例函数y1=$\frac{{k}_{1}}{x}$(其中k1>0)和y2=$\frac{3}{x}$在第一象限内的图象依次是C1和C2,点P在C1上.矩形PCOD交C2于A、B两点,OA的延长线交C1于点E,EF⊥x轴于F点,且图中四边形BOAP的面积为6,则EF:AC为( )
如图,两个反比例函数y1=$\frac{{k}_{1}}{x}$(其中k1>0)和y2=$\frac{3}{x}$在第一象限内的图象依次是C1和C2,点P在C1上.矩形PCOD交C2于A、B两点,OA的延长线交C1于点E,EF⊥x轴于F点,且图中四边形BOAP的面积为6,则EF:AC为( )| A. | $\sqrt{3}$﹕1 | B. | 2﹕$\sqrt{3}$ | C. | 2﹕1 | D. | 29﹕14 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
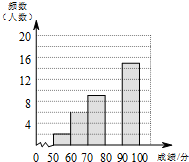 为了传承中华优秀传统文化,某校组织了一次八年级350名学生参加的“汉字听写”大赛,赛后发现所有参赛学生的成绩均不低于50分.为了更好地了解本次大赛的成绩分布情况,随机抽取了其中若干名学生的成绩作为样本进行整理,得到下列不完整的统计图表:
为了传承中华优秀传统文化,某校组织了一次八年级350名学生参加的“汉字听写”大赛,赛后发现所有参赛学生的成绩均不低于50分.为了更好地了解本次大赛的成绩分布情况,随机抽取了其中若干名学生的成绩作为样本进行整理,得到下列不完整的统计图表:| 成绩x/分 | 频数 | 频率 |
| 50≤x<60 | 2 | 0.04 |
| 60≤x<70 | 6 | 0.12 |
| 70≤x<80 | 9 | b |
| 80≤x<90 | a | 0.36 |
| 90≤x≤100 | 15 | 0.30 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com