
”¾ĢāÄæ”æČēĶ¼1ĖłŹ¾£¬ŌŚÕż·½ŠĪABCDÖŠ£¬AB=1£¬ ![]() ŹĒŅŌµćBĪŖŌ²ŠÄ£¬AB³¤ĪŖ°ė¾¶µÄŌ²µÄŅ»¶Ī»”£¬µćEŹĒ±ßADÉĻµÄ¶Æµć£ØµćEÓėµćA£¬D²»ÖŲŗĻ£©£¬¹żE×÷
ŹĒŅŌµćBĪŖŌ²ŠÄ£¬AB³¤ĪŖ°ė¾¶µÄŌ²µÄŅ»¶Ī»”£¬µćEŹĒ±ßADÉĻµÄ¶Æµć£ØµćEÓėµćA£¬D²»ÖŲŗĻ£©£¬¹żE×÷![]() ĖłŌŚŌ²µÄĒŠĻߣ¬½»±ßDCÓŚµćF£¬GĪŖĒŠµć£®
ĖłŌŚŌ²µÄĒŠĻߣ¬½»±ßDCÓŚµćF£¬GĪŖĒŠµć£®
£Ø1£©ĒóÖ¤£ŗEA=EG£»
£Ø2£©ÉčAE=x£¬FC=y£¬Ēóy¹ŲÓŚxµÄŗÆŹż¹ŲĻµŹ½£¬²¢Ö±½ÓŠ“³öxµÄȔֵ·¶Ī§£»
£Ø3£©ČēĶ¼2ĖłŹ¾£¬½«”÷DEFŃŲÖ±ĻßEF·ÕŪŗóµĆ”÷D1EF£¬Į¬½ÓAD1£¬D1D£¬ŹŌĢ½Ė÷£ŗµ±µćEŌĖ¶Æµ½ŗĪ“¦Ź±£¬”÷AD1DÓė”÷ED1FĻąĖĘ£æĒėĖµĆ÷ĄķÓÉ£®
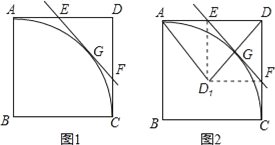
”¾“š°ø”æ£Ø1£©Ö¤Ć÷¼ū½āĪö£»£Ø2£©y=![]() £Ø0£¼x£¼1£©£»£Ø3£©µ±µćEŌĖ¶Æµ½ADµÄÖŠµćŹ±£¬”÷AD1DÓė”÷ED1FĻąĖĘ£»ĄķÓɼū½āĪö£®
£Ø0£¼x£¼1£©£»£Ø3£©µ±µćEŌĖ¶Æµ½ADµÄÖŠµćŹ±£¬”÷AD1DÓė”÷ED1FĻąĖĘ£»ĄķÓɼū½āĪö£®
”¾½āĪö”æŹŌĢā·ÖĪö£ŗ£Ø1£©Ö¤³öADŹĒŌ²BµÄĒŠĻߣ¬ÓÉĒŠĻß³¤¶ØĄķ¼“æÉµĆ³ö½įĀŪ£»
£Ø2£©øł¾ŻĒŠĻß³¤¶ØĄķ”¢Õż·½ŠĪµÄŠŌÖŹµĆµ½ÓŠ¹ŲµÄĻ߶ĪÓĆx£¬y±ķŹ¾£¬ŌŁøł¾Ż¹“¹É¶ØĄķ½ØĮ¢ŗÆŹż¹ŲĻµŹ½£®
£Ø3£©øł¾ŻĒŠĻß³¤¶ØĄķÕŅµ½½ĒÖ®¼äµÄ¹ŲĻµ£¬“Ó¶ų·¢ĻÖÕż·½ŠĪ£¬øł¾ŻÕż·½ŠĪµÄŠŌÖŹµĆµ½Į½øö½Ē¶ŌÓ¦ĻąµČ£¬“Ó¶ųÖ¤Ć÷Čż½ĒŠĪĻąĖĘ£®
ŹŌĢā½āĪö£ŗ£Ø1£©”ßĖıߊĪABCDŹĒÕż·½ŠĪ£¬”ą”ĻBAD=”ĻD=90”ć£¬AD=CD=AB=1£¬”ąAD”ĶBA£¬”ąADŹĒŌ²BµÄĒŠĻߣ¬”ßEGŹĒŌ²BµÄĒŠĻߣ¬”ąEA=EG£»
£Ø2£©”ßEFĒŠŌ²BÓŚµćG£¬”ąEA=EG£¬FC=FG£®
”ßAE=x£¬FC=y”ąEF=x+y£¬DE=1©x£¬DF=1©y£¬
ŌŚRt”÷DEFÖŠ£¬øł¾Ż¹“¹É¶ØĄķ£¬µĆ£ŗ£Øx+y£©2=£Ø1©x£©2+£Ø1©y£©2
”ąy=![]() £Ø0£¼x£¼1£©£®
£Ø0£¼x£¼1£©£®
£Ø3£©µ±µćEŌĖ¶Æµ½ADµÄÖŠµćŹ±£¬”÷AD1DÓė”÷ED1FĻąĖĘ£»ĄķÓÉČēĻĀ£ŗ
ÉčÖ±ĻßEF½»Ļ߶ĪDD1ÓŚµćH£¬ÓÉĢāŅā£¬µĆ£ŗ”÷EDF”Õ”÷ED1F£¬EF”ĶDD1ĒŅDH=D1H£®
”ßAE=![]() £¬AD=1£¬”ąAE=ED£®”ąEH”ĪAD1£¬”ĻAD1D=”ĻEHD=90”ć£®
£¬AD=1£¬”ąAE=ED£®”ąEH”ĪAD1£¬”ĻAD1D=”ĻEHD=90”ć£®
Ó֔ߔĻED1F=”ĻEDF=90”ć£¬”ą”ĻFD1D=”ĻAD1D£®”ąD1F”ĪAD£¬”ą”ĻADD1=”ĻDD1F=”ĻEFD=45”ć£¬
”ą”÷ED1F”×”÷AD1D£®



 ŌĶĮæģ³µĻµĮŠ“š°ø
ŌĶĮæģ³µĻµĮŠ“š°ø
| Äź¼¶ | øßÖŠæĪ³Ģ | Äź¼¶ | ³õÖŠæĪ³Ģ |
| øßŅ» | øßŅ»Ćā·ŃæĪ³ĢĶĘ¼ö£” | ³õŅ» | ³õŅ»Ćā·ŃæĪ³ĢĶĘ¼ö£” |
| ø߶ž | ø߶žĆā·ŃæĪ³ĢĶĘ¼ö£” | ³õ¶ž | ³õ¶žĆā·ŃæĪ³ĢĶĘ¼ö£” |
| øßČż | øßČżĆā·ŃæĪ³ĢĶĘ¼ö£” | ³õČż | ³õČżĆā·ŃæĪ³ĢĶĘ¼ö£” |
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
”¾ĢāÄæ”æŅŃÖŖ£ŗŹµŹża£¬bŌŚŹżÖįÉĻµÄĪ»ÖĆČēĶ¼ĖłŹ¾£¬»Æ¼ņ£ŗ ![]() ©|a©b|£®
©|a©b|£®![]()
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
”¾ĢāÄæ”æŅŃÖŖ£¬A”¢BĮ½µŲĻą¾ą120Ē§Ć×£¬¼×Ęļ×ŌŠŠ³µŅŌ20Ē§Ć×/Ź±µÄĖŁ¶ČÓÉĘšµćAĒ°ĶłÖÕµćB£¬ŅŅĘļĦĶŠ³µŅŌ40Ē§Ć×/Ź±µÄĖŁ¶ČÓÉĘšµćBĒ°ĶłÖÕµćA£®Į½ČĖĶ¬Ź±³ö·¢£¬ø÷×Ōµ½“ļÖÕµćŗóĶ£Ö¹£®ÉčĮ½ČĖÖ®¼äµÄ¾ąĄėĪŖs£ØĒ§Ć×£©£¬¼×ŠŠŹ»µÄŹ±¼äĪŖt£ØŠ”Ź±£©£¬ŌņĻĀĶ¼ÖŠÕżČ··“Ó³sÓėtÖ®¼äŗÆŹż¹ŲĻµµÄŹĒ£Ø £©
A.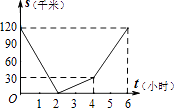
B.
C.
D.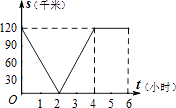
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
”¾ĢāÄæ”æČēĶ¼1ĖłŹ¾£¬ŌŚA£¬BĮ½µŲÖ®¼äÓŠĘū³µÕ¾CÕ¾£¬æĶ³µÓÉAµŲŹ»ĶłCÕ¾£¬»õ³µÓÉBµŲŹ»ĶłAµŲ£®Į½³µĶ¬Ź±³ö·¢£¬ŌČĖŁŠŠŹ»£®Ķ¼2ŹĒæĶ³µ”¢»õ³µĄėCÕ¾µÄĀ·³Ģy1 £¬ y2£ØĒ§Ć×£©ÓėŠŠŹ»Ź±¼äx£ØŠ”Ź±£©Ö®¼äµÄŗÆŹż¹ŲĻµĶ¼Ļó£®
£Ø1£©ĢīæÕ£ŗA£¬BĮ½µŲĻą¾ąĒ§Ć×£»
£Ø2£©ĒóĮ½Š”Ź±ŗ󣬻õ³µĄėCÕ¾µÄĀ·³Ģy2ÓėŠŠŹ»Ź±¼äxÖ®¼äµÄŗÆŹż¹ŲĻµŹ½£»
£Ø3£©µ±æĶ³µŠŠŹ»¶ą³¤Ź±¼ä£¬æĶ”¢»õĮ½³µĻą¾ą150Ē§Ć×.
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
”¾ĢāÄæ”æČēĶ¼£¬E”¢F·Ö±šŹĒ”õABCDµÄ±ßBC”¢ADÉĻµÄµć£¬ĒŅBE£½DF£®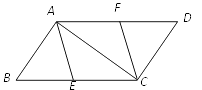
£Ø1£©ĒóÖ¤£ŗĖıߊĪAECFŹĒĘ½ŠŠĖıߊĪ£»
£Ø2£©ČōBC£½10£¬”ĻBAC£½90”ć£¬ĒŅĖıߊĪAECFŹĒĮāŠĪ£¬ĒóBEµÄ³¤£®
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
”¾ĢāÄæ”æČēĶ¼£¬ŅŃÖŖ”ŃOµÄÖ±¾¶CD“¹Ö±ÓŚĻŅAB£¬“¹×ćĪŖµćE£¬”ĻACD=22.5”ć£¬ČōCD=6cm£¬ŌņABµÄ³¤ĪŖ£Ø””””£©
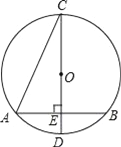
A. 4cm B. 3![]() cm C. 2
cm C. 2![]() cm D. 2
cm D. 2![]() cm
cm
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
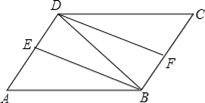
”¾ĢāÄæ”æČēĶ¼£¬ŌŚABCDÖŠ£¬”ĻABDµÄĘ½·ÖĻßBE½»ADÓŚµćE£¬”ĻCDBµÄĘ½·ÖĻßDF½»BCÓŚµćF£®ĒóÖ¤£ŗ”÷ABE”Õ”÷CDF£®
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
”¾ĢāÄæ”æČēĶ¼£¬ŌŚ”÷ABCÖŠ£¬AB=AC£¬DĪŖBC±ßÉĻŅ»µć£¬”ĻB=30”ć£¬”ĻDAB=45”ć£®ĒóÖ¤£ŗAC=DC£® 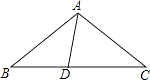
²éæ““š°øŗĶ½āĪö>>
°Ł¶ČÖĀŠÅ - Į·Ļ°²įĮŠ±ķ - ŹŌĢāĮŠ±ķ
ŗž±±Ź”»„ĮŖĶųĪ„·ØŗĶ²»Į¼ŠÅĻ¢¾Ł±ØĘ½ĢØ | ĶųÉĻÓŠŗ¦ŠÅĻ¢¾Ł±Ø×ØĒų | µēŠÅÕ©Ę¾Ł±Ø×ØĒų | É꥜Ź·ŠéĪŽÖ÷ŅåÓŠŗ¦ŠÅĻ¢¾Ł±Ø×ØĒų | ÉęĘóĒÖČؾŁ±Ø×ØĒų
Ī„·ØŗĶ²»Į¼ŠÅĻ¢¾Ł±Øµē»°£ŗ027-86699610 ¾Ł±ØÓŹĻä£ŗ58377363@163.com