
 填空:
填空: 口算题天天练系列答案
口算题天天练系列答案科目:初中数学 来源: 题型:选择题
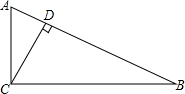 如图,在△ABC中,∠ACB=90°,CD为高,AC=4,则下列计算结果错误的是( )
如图,在△ABC中,∠ACB=90°,CD为高,AC=4,则下列计算结果错误的是( )| A. | 若BC=3,则CD=2.4 | B. | 若∠A=30°,则BD=$\frac{\sqrt{3}}{3}$ | ||
| C. | 若∠A=45°,则AD=2$\sqrt{2}$ | D. | 若BC=2,则S△ADC=$\frac{16}{5}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,在菱形ABCD中,∠B=60°,AB=1,延长AD到点E,使DE=AD,延长CD到点F,使DF=CD,连接AC、CE、EF、AF.
如图,在菱形ABCD中,∠B=60°,AB=1,延长AD到点E,使DE=AD,延长CD到点F,使DF=CD,连接AC、CE、EF、AF.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
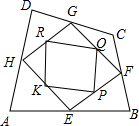 如图,铎山中心学校校园内有一块四边形空地ABCD,学校征集对这块空地种植的花草的设计中,选定如下方案:把这个四边形分成九块,种植三种不同的花草,其中E、F、G、H分别是AB、BC、CD、DA的中点,P、Q、R、K分别是EF、FG、GH、HE的中点,现要在四边形PQRK中种上红色的花,在△PFQ、△QGR、△RHK、△KEP中种上黄色的花,在△HAE、△EBF、△FCG、△GDH中种上紫色的花.已知种红、黄、紫三种花的单价分别为10元/m2、12元/m2、14元/m2,而种红花已用去了120元.请你用学过的数学知识计算出种满四边形ABCD这块空地的花共需要多少元?
如图,铎山中心学校校园内有一块四边形空地ABCD,学校征集对这块空地种植的花草的设计中,选定如下方案:把这个四边形分成九块,种植三种不同的花草,其中E、F、G、H分别是AB、BC、CD、DA的中点,P、Q、R、K分别是EF、FG、GH、HE的中点,现要在四边形PQRK中种上红色的花,在△PFQ、△QGR、△RHK、△KEP中种上黄色的花,在△HAE、△EBF、△FCG、△GDH中种上紫色的花.已知种红、黄、紫三种花的单价分别为10元/m2、12元/m2、14元/m2,而种红花已用去了120元.请你用学过的数学知识计算出种满四边形ABCD这块空地的花共需要多少元?查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com