
����Ŀ����ͼ���ڵ���Rt��ABC�У���C=90�㣬AC=8��F��AB���ϵ��е㣬��D��E�ֱ���AC��BC�����˶����ұ���AD=CE������DE��DF��EF���ڴ��˶��仯�Ĺ����У����н��ۣ�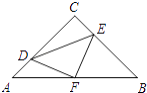
�١�DFE�ǵ���ֱ�������Σ�
���ı���CDFE������Ϊ�����Σ�
��DE���ȵ���СֵΪ4��
���ı���CDFE��������ֲ��䣻
�ݡ�CDE��������ֵΪ8��
������ȷ�Ľ����ǣ� ��
A.�٢ڢ�
B.�٢ܢ�
C.�٢ۢ�
D.�ۢܢ�
���𰸡�B
���������⣺����CF��
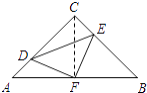
�ߡ�ABC�ǵ���ֱ�������Σ�
���FCB=��A=45�㣬CF=AF=FB��
��AD=CE��
���ADF�ա�CEF��SAS����
��EF=DF����CFE=��AFD��
�ߡ�AFD+��CFD=90�㣬
���CFE+��CFD=��EFD=90�㣬
���EDF�ǵ���ֱ�������Σ��ʢ���ȷ����
��D��E�ֱ�ΪAC��BC�е�ʱ���ı���CDFE�������Σ��ʢڴ���
�ߡ�ADF�ա�CEF��
��S��CEF=S��ADF
��S�ı���CEFD=S��AFC�����ʢ���ȷ����
���ڡ�DEF�ǵ���ֱ�������Σ���˵�DE��Сʱ��DFҲ��С��
����DF��ACʱ��DE��С����ʱDF= ![]() BC=4��
BC=4��
��DE= ![]() DF=4
DF=4 ![]() ���ʢ۴���
���ʢ۴���
����CDE������ʱ���ɢ�֪����ʱ��DEF�������С��
��ʱS��CDE=S�ı���CEFD��S��DEF=S��AFC��S��DEF=16��8=8���ʢ���ȷ����
��B��������.
�ʴ�Ϊ��B��
����CF.��֤����ADF�ա�CEF�ɵ�EF=DF����CFE=��AFD�����ɡ�AFD+��CFD=90��ɵá�EFD=90�㣬�Ӷ��жϢ٣�
��D��E�ֱ�ΪAC��BC�е�ʱ���ı���CDFE�������Σ��Ӷ��жϢڣ�
���ڡ�DEF�ǵ���ֱ�������Σ���˵�DE��Сʱ��DFҲ��С������DF��ACʱ��DE��С���Ӷ����DF��ֵ�������ɵ�DE��ֵ�����жϢۣ�
�ɡ�ADF�ա�CEF�ɵ�S�ı���CEFD=S��AFC���Ӷ��жϢܣ�
�ɢ�֪����ʱ��DEF�������С����ʱS��CDE=S�ı���CEFD��S��DEF=S��AFC��S��DEF���Ӷ������CDE����������жϢ�.



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪���߶�![]() ��
��![]() ��
��![]() ��
��
��������ABC��ʹ![]() ��
�� ![]() ��
�� ![]() ��
��

���𰸡��𰸼�����
������������������Ȼ�����![]() ��ȵĽǣ��ٻ���
��ȵĽǣ��ٻ���![]() �ij�������
�ij�������![]() ����
����![]() ������������
������������
�����������ͼ��ʾ�����Ȼ�����BC��
�������Ķ���ΪԲ��,���ⳤΪ�뾶����,�ֱ��������߽���ΪA��,C����
������ͬ����Ϊ�뾶,BΪԲ��,����,��BC�ڵ�F,��FΪԲ��,C��A��Ϊ�뾶���������ڵ�E��
����BF��ȡ��C��ʹCB=a����BΪԲ�ģ�cΪ�뾶��Բ��BE���ӳ����ڵ�A������AC��
���ۣ���ABC��Ϊ����������.

�����͡������
��������
15
����Ŀ����֪���߶�![]() ��
�� ![]() ��������
�������� ![]() ��ʹ
��ʹ![]() ��
�� ![]() ��
��

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��һ�������ߣ�y=��x��x��2����0��x��2����ΪC1 �� ����x�ύ������O��A1����C1��A1��ת180��õ�C2 �� ��x����A2����C2��A2��ת180��õ�C3 �� ��x����A3������˽�����ȥ��ֱ���õ�C2017 �� ����P�ǵ�2016�������ߵĶ��㣬��P�������Ϊ �� 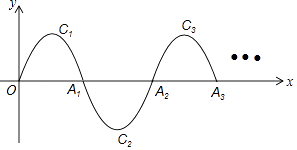
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ������ABC�ı߳�Ϊ2����BC���ϵĸ�AB1Ϊ��������AB1C1����ABC���AB1C1�������ֵ������ΪS1����������AB1C1��B1C1�ϵĸ�AB2Ϊ��������AB2C2����AB1C1���AB2C2�������ֵ������ΪS2�������Դ����ƣ���Sn=____�����ú�n��ʽ�ӱ�ʾ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��һ���̵�Ҫ����װ�ޣ�����ס�������װ����ͬʱʩ����8�������ɣ��踶������ù�3520Ԫ����������鵥����6�죬�������鵥����12�����ɣ��踶������ù�3480Ԫ���ʣ�
(1)�ס������鹤��һ�죬�̵�Ӧ��������Ԫ��
(2)��֪���鵥������12����ɣ����鵥������24����ɣ����������飬�̵������������٣�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���ڳ����ۺ���������������Ϊ���˽��꼶������������ֶԳ���ij���ѧ�������������ȼ��ĵ��飬������������Ů���ȼ��������ͳ��ͼ��ȫ��ȼ��������ͳ��ͼ�� 
��1�����鷢�������ȼ�Ϊ�ϸ��������2�ˣ�Ů����1�ˣ���ȫ�����ѧ����
��2����ȫŮ���ȼ�����������ͳ��ͼ��
��3�����ݵ���������ð�����δ������ȼ�Ϊ�ϸ��A��ѧ���и�ѡ1��ѧ�����н�������������ͼ���������պ�ѡ��һ��������һ��Ů���ĸ��ʣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ������ABC �У��� D��E �ֱ��ڱ� AC��AB �ϣ�BD �� CE ���ڵ� O���������������������١�EBO����DCO����BE��CD����OB��OC��
(1)�������������У������������������ж���ABC �ǵ��������Σ�(�����д�����г���������)
(2)��ѡ��(1)�е�һ�����Σ�д��֤�����̣�

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��������OABC�ı�OA�������ϣ�OΪԭ�㣬������OABC�����Ϊ12��OC�߳�Ϊ3.
(1)д�������ϵ�A��ʾ������
(2)��������OABC����������ˮƽ�ƶ����ƶ���ij����μ�Ϊ![]() �����ƶ���ij�����
�����ƶ���ij�����![]() ��ԭ������OABC�ص����ֵ����ǡ�õ���ԭ������OABC�����
��ԭ������OABC�ص����ֵ����ǡ�õ���ԭ������OABC�����![]() ʱ��д�������ϵ�
ʱ��д�������ϵ�![]() ��ʾ������
��ʾ������

�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com