
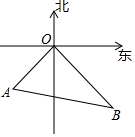
 如图,甲轮船以24海里/小时的速度离开港口O向东南方向航行,乙轮船同时同地以18海里/小时的速度向西南方向航行,已知他们离开港口半小时后分别到达B,A两地,求A,B两地之间的距离.
如图,甲轮船以24海里/小时的速度离开港口O向东南方向航行,乙轮船同时同地以18海里/小时的速度向西南方向航行,已知他们离开港口半小时后分别到达B,A两地,求A,B两地之间的距离. 科目:初中数学 来源: 题型:填空题
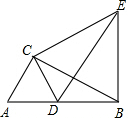 如图,Rt△ABC中,∠ACB=90°,∠ABC=30°,AC=1,将△ABC绕点C逆时针旋转至△CDE,使得点D恰好落在AB上,连接BE,则BE的长度为$\sqrt{3}$.
如图,Rt△ABC中,∠ACB=90°,∠ABC=30°,AC=1,将△ABC绕点C逆时针旋转至△CDE,使得点D恰好落在AB上,连接BE,则BE的长度为$\sqrt{3}$.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
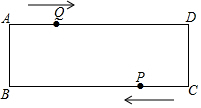 如图,在矩形ABCD中,AB=1cm,AD=3cm,点Q从A点出发,以1cm/s的速度沿AD向终点D运动,点P从点C出发,以1cm/s的速度沿CB向终点B运动,当这两点中有一点到达自己的终点时,另一点也停止运动,两点同时出发,运动了t秒.
如图,在矩形ABCD中,AB=1cm,AD=3cm,点Q从A点出发,以1cm/s的速度沿AD向终点D运动,点P从点C出发,以1cm/s的速度沿CB向终点B运动,当这两点中有一点到达自己的终点时,另一点也停止运动,两点同时出发,运动了t秒.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 10 | B. | 4 | C. | 4或-6 | D. | 4或-6或10 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | $\sqrt{8}$ | B. | $\sqrt{10}$ | C. | $\sqrt{20}$ | D. | $\sqrt{\frac{1}{3}}$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com