
���� ��1�������ȳ˷����ٳ˳���˳��ֱ�ӽ��м��㣻
��2�����ĸ��ʽ��Ӽ�����ͨ�֣���Ϊͬ��ĸ�ķ�ʽ��Ȼ���ٰ�ͬ��ĸ��ʽ�ļӼ���������м��㣮
��3��ֱ��������ʽ�ij���������м��㣻
��4�����ݷ�ʽ�����㷨����л���Ȼ���x��ֵ������㣮
��� �⣺��1��ԭʽ=$\frac{{a}^{4}{b}^{2}}{{c}^{2}}$•c4•$\frac{{a}^{4}}{{b}^{4}{c}^{4}}$
=$\frac{{a}^{8}}{{b}^{2}{c}^{2}}$��
��2��ԭʽ=$\frac{2a}{��a+2����a-2��}$-$\frac{a+2}{��a+2����a-2��}$
=$\frac{1}{a+2}$��
��3��ԭʽ=$\frac{a+1}{a-2}$•$\frac{��a+2����a-2��}{a+1}$
=a+2��
��4����$\frac{x+1}{x-1}$+$\frac{1}{{x}^{2}-2x+1}$����$\frac{x}{x-1}$
=$\frac{x}{��x-1��^{2}}$•$\frac{x-1}{x}$
=$\frac{1}{x-1}$��
��x=$\sqrt{2}$+1ʱ��ԭʽ=$\frac{1}{\sqrt{2}+1-1}$=$\frac{\sqrt{2}}{2}$��
���� ���⿼���˶���ʽ�ij˷������ij˷������ʣ�����ʽ�ij˷�������ʽ�ij�������ʽ�ļӼ����Լ�������㣬�����������㷨���ǽⱾ��Ĺؼ���


 ѧ���������ν��Ͼ���ѧ������ϵ�д�
ѧ���������ν��Ͼ���ѧ������ϵ�д� Happy holiday���ּ��������ҵ�㶫���������ϵ�д�
Happy holiday���ּ��������ҵ�㶫���������ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
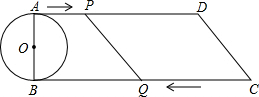 ��ͼ����ֱ֪������ABCD�У�AD��BC����B=90�㣬AB=8cm��AD=24cm��BC=26cm��ABΪ��O��ֱ��������P�ӵ�A��ʼ��AD�����D��1cm/s���ٶ��˶�������Q�ӵ�C��ʼ��CB�����B��3cm/s�ٶ��˶���P��Q�ֱ�ӵ�A��Cͬʱ������������һ�㵽���յ�ʱ����һ��Ҳ��ֹ֮ͣ�˶������˶�ʱ��Ϊt s���ʣ�
��ͼ����ֱ֪������ABCD�У�AD��BC����B=90�㣬AB=8cm��AD=24cm��BC=26cm��ABΪ��O��ֱ��������P�ӵ�A��ʼ��AD�����D��1cm/s���ٶ��˶�������Q�ӵ�C��ʼ��CB�����B��3cm/s�ٶ��˶���P��Q�ֱ�ӵ�A��Cͬʱ������������һ�㵽���յ�ʱ����һ��Ҳ��ֹ֮ͣ�˶������˶�ʱ��Ϊt s���ʣ��鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
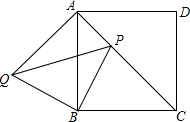 ��ͼ����������ABCD�У���P�ǶԽ���AC��һ�㣬�ѡ�BPC���ŵ�B��ʱ����ת�õ���BQA��
��ͼ����������ABCD�У���P�ǶԽ���AC��һ�㣬�ѡ�BPC���ŵ�B��ʱ����ת�õ���BQA���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | -a��-b | B�� | 4a��4b | C�� | 2a-1��3b-1 | D�� | a+3��b+3 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
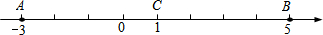
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | Բ | B�� | ������ | C�� | �� | D�� | ������ |
�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com