
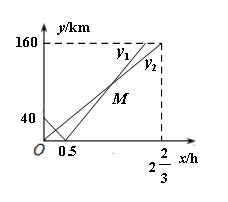
ij�κ�����ͧ��ϰ�У��ס�������ͧͬʱ��A��B�����ۿڳ���������ֱ������ʻ����ϰĿ��غ���C������ͧ������C������ϰ��һ�ν���.��֪B��λ��A�ۡ�C��֮�䣬��A��B��C��һ��ֱ����. ��ס�������ͧ��ʻx(h)����B�۵ľ���ֱ�Ϊy1��y2(km)��y1��y2��x�ĺ�����ϵ��ͼ��ʾ.
��1����A����C��֮��ľ��룻
��2���ֱ� ����ס�������ͧ�ĺ��ټ�ͼ�е�M�����ꣻ
����ס�������ͧ�ĺ��ټ�ͼ�е�M�����ꣻ
��3�����ס�������֮ͧ��ľ��벻����20kmʱ���������ͨѶ���룬���������ͧ����ϰ��һ�δ������ͨѶ����ʱ��x��ȡֵ��Χ.
 |

| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
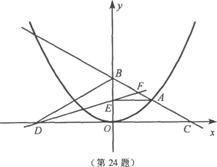
��ͼ����ƽ��ֱ������ϵ�У�A��������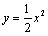 �ϵ�һ�����㣬�ҵ�A�ڵ�һ�����ڣ�AE��y���ڵ�E����B����Ϊ(O��2)��ֱ��AB��
�ϵ�һ�����㣬�ҵ�A�ڵ�һ�����ڣ�AE��y���ڵ�E����B����Ϊ(O��2)��ֱ��AB�� ���ڵ�C����D���C����y��Գƣ�ֱ��DE��AB�ཻ�ڵ�F������BD�����߶�AE�ij�Ϊ
���ڵ�C����D���C����y��Գƣ�ֱ��DE��AB�ཻ�ڵ�F������BD�����߶�AE�ij�Ϊ ����BED�����ΪS��
����BED�����ΪS��
(1)��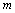 ��
��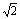 ʱ����S��ֵ��
ʱ����S��ֵ��
(2)��S����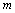 (
(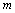 ��2)�ĺ�������ʽ��
��2)�ĺ�������ʽ��
(3)����S��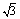 ʱ����
ʱ����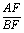 ��ֵ��
��ֵ��
�ڵ�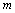 ��2ʱ����
��2ʱ����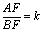 ������
������ ��
�� ��������ϵ��֤����
��������ϵ��֤����
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
��֪������y=x2��2x��3������P����2��5�����Q���ڸ������ߵĶԳ���Գƣ����Q��������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
�ײ��������� �����ֱ��������1��2��3���Ҳ��������������ֱ��������2��3��4����Щ�����ɫ����������ȫ��ͬ��С���Ӽ״����������һ������С�մ��Ҵ����������һ������
�����ֱ��������1��2��3���Ҳ��������������ֱ��������2��3��4����Щ�����ɫ����������ȫ��ͬ��С���Ӽ״����������һ������С�մ��Ҵ����������һ������
��1���û���״ͼ������ͼ�����б��ķ��������������������ϵ�����֮��Ϊ6�ĸ��ʣ�
��2��С����С������Ϸ�������ǣ����������������ϵ�����֮��Ϊ������С��ʤ������С��ʤ������Ϊ�����Ϸ��ƽ��Ϊʲô��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
ƽ���ı��εĶԽ���һ�����е�������( )
A����� B������ƽ�� C�� ���ഹֱ D�����ഹֱ�����
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
��ͼ��ijС���滮��һ����30m����20m�ij�����ABCD��������ͬ������ͨ����ʹ����������ABƽ�У���һ����ADƽ�У����ಿ���ֻ��ݡ�Ҫʹÿһ�黨�ݵ������Ϊ78m2����ôͨ���Ŀ�Ӧ��Ƴɶ���m����ͨ���Ŀ�Ϊ
 m���������е÷���
m���������е÷���

�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com