
【题目】某校为了解学生对“防溺水”安全知识的掌握情况,从全校![]() 名学生中随机抽取部分学生进行测试,并将测试成绩(百分制,得分均为整数)进行统计分析,绘制了如下不完整的频数表和频数直方图.
名学生中随机抽取部分学生进行测试,并将测试成绩(百分制,得分均为整数)进行统计分析,绘制了如下不完整的频数表和频数直方图.
被抽取的部分学生安全知识测试成绩频数表
组别 | 成绩(分) | 频数(人) | 频率 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
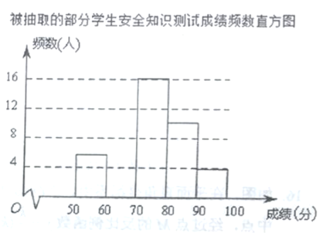
由图表中给出的信息回答下列问题:
![]() 表中的
表中的![]() ;抽取部分学生的成绩的中位数在 组;
;抽取部分学生的成绩的中位数在 组;
![]() 把上面的频数直方图补充完整;
把上面的频数直方图补充完整;
![]() 如果成绩达到
如果成绩达到![]() 分以上(包括
分以上(包括![]() 分)为优秀,请估计该校
分)为优秀,请估计该校![]() 名学生中成绩优秀的人数.
名学生中成绩优秀的人数.
 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
【题目】一笔总额为![]() 元的奖金,分为一等奖、二等奖和三等奖,奖金金额均为整数,每个一等奖的奖金是每个二等奖奖金的两倍,每个二等奖的奖金是每个三等奖奖金的两倍,若把这笔奖金发给
元的奖金,分为一等奖、二等奖和三等奖,奖金金额均为整数,每个一等奖的奖金是每个二等奖奖金的两倍,每个二等奖的奖金是每个三等奖奖金的两倍,若把这笔奖金发给![]() 个人,评一、二、三等奖的人数分别为
个人,评一、二、三等奖的人数分别为![]() ,且
,且![]() ,那么三等奖的奖金金额是_______元.
,那么三等奖的奖金金额是_______元.
查看答案和解析>>
科目:初中数学 来源: 题型:
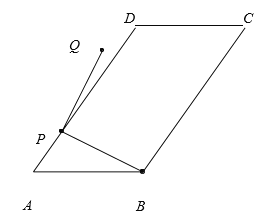
【题目】如图,在平行四边形ABCD中,AB=10,BC=15,tan∠A=![]() 点P为AD边上任意一点,连结PB,将PB绕点P逆时针旋转90°得到线段PQ.若点Q恰好落在平行四边形ABCD的边所在的直线上,则PB旋转到PQ所扫过的面积____(结果保留π)
点P为AD边上任意一点,连结PB,将PB绕点P逆时针旋转90°得到线段PQ.若点Q恰好落在平行四边形ABCD的边所在的直线上,则PB旋转到PQ所扫过的面积____(结果保留π)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】五张完全相同的卡片的正面分别画有等边三角形、平行四边形、矩形、菱形、正方形,将其背面朝上放在桌面上,从中随机抽取一张,所抽取的卡片上的图形既是轴对称图形,又是中心对称图形的概率是( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
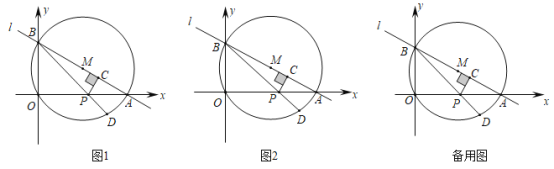
【题目】如图1,直线![]() 与
与![]() 轴交于点
轴交于点![]() ,与
,与![]() 轴交于点
轴交于点![]() ,以
,以![]() 为直径作
为直径作![]() ,点
,点![]() 为线段
为线段![]() 上一动点(与点O、A不重合),作
上一动点(与点O、A不重合),作![]() 于
于![]() ,连结
,连结![]() 并延长交
并延长交![]() 于点
于点![]() .
.
(1)求点![]() 的坐标和
的坐标和![]() 的值;
的值;
(2)设![]() .
.
①当![]() 时,求
时,求![]() 的值及点
的值及点![]() 的坐标;
的坐标;
②求![]() 关于
关于![]() 的函数表达式.
的函数表达式.
(3)如图2,连接![]() ,当点
,当点![]() 在线段
在线段![]() 上运动时,求
上运动时,求![]() 的最大值.
的最大值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系![]() 中,抛物线
中,抛物线![]() ,与x轴交于A、B两点(点A在点B的左侧).
,与x轴交于A、B两点(点A在点B的左侧).
(1)求点A和点B的坐标;
(2)若点P(m,n)是抛物线上的一点,过点P作x轴的垂线,垂足为点D.
①在![]() 的条件下,当
的条件下,当![]() 时,n的取值范围是
时,n的取值范围是![]() ,求抛物线的表达式;
,求抛物线的表达式;
②若D点坐标(4,0),当![]() 时,求a的取值范围.
时,求a的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
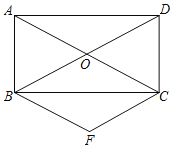
【题目】如图,矩形ABCD的对角线AC,BD相交于点O,过B点作BF∥AC,过C点作CF∥BD,BF与CF相交于点F.
(1)求证:四边形BFCO是菱形;
(2)连接OF、DF,若AB=2,tan∠OFD=![]() ,求AC的长.
,求AC的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系![]() 中,点
中,点![]() ,若射线
,若射线![]() 上存在点
上存在点![]() ,使得
,使得![]() 是以
是以![]() 为腰的等腰三角形,就称点
为腰的等腰三角形,就称点![]() 为线段
为线段![]() 关于射线
关于射线![]() 的等腰点.
的等腰点.
(1)如图, ![]() ,
,
①若![]() ,则线段
,则线段![]() 关于射线
关于射线![]() 的等腰点的坐标是_____;
的等腰点的坐标是_____;
②若![]() ,且线段
,且线段![]() 关于射线
关于射线![]() 的等腰点的纵坐标小于1,求
的等腰点的纵坐标小于1,求![]() 的取值范围;
的取值范围;
(2) 若![]() ,且射线
,且射线![]() 上只存在一个线段
上只存在一个线段![]() 关于射线
关于射线![]() 的等腰点,则
的等腰点,则![]() 的取值范围是__________.
的取值范围是__________.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com