
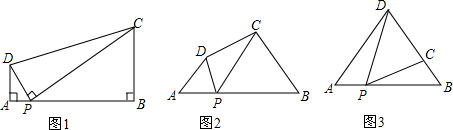
分析 (1)由∠DPC=∠A=∠B=90°可得∠ADP=∠BPC,即可证到△ADP∽△BPC,然后运用相似三角形的性质即可解决问题;
(2)由∠DPC=∠A=∠B=α可得∠ADP=∠BPC,即可证到△ADP∽△BPC,然后运用相似三角形的性质即可解决问题;
(3)过点D作DE⊥AB于点E,根据等腰三角形的性质可得AE=BE=3,根据勾股定理可得DE=4,由题可得DC=DE=4,则有BC=5-4=1.易证∠DPC=∠A=∠B.根据AD•BC=AP•BP,就可求出t的值.
解答 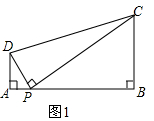 (1)证明:如图1,
(1)证明:如图1,
∵∠DPC=∠A=∠B=90°,
∴∠ADP+∠APD=90°,
∠BPC+∠APD=90°,
∴∠APD=∠BPC,
∴△ADP∽△BPC,
∴$\frac{AD}{BP}$=$\frac{AP}{BC}$,
∴AD•BC=AP•BP;
(2)结论AD•BC=AP•BP仍成立;
理由:如图2,∵∠BPD=∠DPC+∠BPC,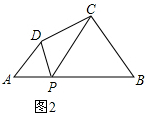
又∵∠BPD=∠A+∠APD,
∴∠DPC+∠BPC=∠A+∠APD,
∵∠DPC=∠A=α,
∴∠BPC=∠APD,
又∵∠A=∠B=α,
∴△ADP∽△BPC,
∴$\frac{AD}{BP}$=$\frac{AP}{BC}$,
∴AD•BC=AP•BP;
(3)解:如图3,过点D作DE⊥AB于点E,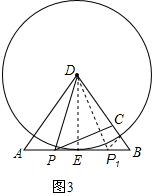
∵AD=BD=5,AB=6,
∴AE=BE=3
∴DE=$\sqrt{{5}^{2}-{3}^{2}}$=4,
∵以D为圆心,以DC为半径的圆与AB相切,
∴DC=DE=4,
∴BC=5-4=1,
∵AD=BD,
∴∠A=∠B,
又∵∠DPC=∠A,
∴∠DPC=∠A=∠B,
由(1)(2)的经验得AD•BC=AP•BP,
又∵AP=t,BP=6-t,
∴t(6-t)=5×1,
∴解得:t1=1,t2=5,
∴t的值为1秒或5秒.
点评 本题考查了相似三角形的判定与性质、切线的性质、等腰三角形的性质、勾股定理、三角形外角的性质、解一元二次方程等知识,培养学生运用已有经验解决问题的能力,渗透了特殊到一般的思想.


 小天才课时作业系列答案
小天才课时作业系列答案 一课四练系列答案
一课四练系列答案 黄冈小状元满分冲刺微测验系列答案
黄冈小状元满分冲刺微测验系列答案 新辅教导学系列答案
新辅教导学系列答案 阳光同学一线名师全优好卷系列答案
阳光同学一线名师全优好卷系列答案科目:初中数学 来源: 题型:解答题
 如图,有一块直角三角形纸片,两直角边AC=7cm,BC=24cm,现将直角边AC沿直线AD折叠,使它恰好落在斜边AB上,且与AE重合,求CD的长.
如图,有一块直角三角形纸片,两直角边AC=7cm,BC=24cm,现将直角边AC沿直线AD折叠,使它恰好落在斜边AB上,且与AE重合,求CD的长.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 不等式x<5的整数解有无数多个 | B. | 不等式-2x<8的解集是x<-4 | ||
| C. | 不等式x>-5的负整数解是有限个 | D. | -40是不等式2x<-8的一个解 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com