
【题目】如图,在平面直角坐标系中,点A,B的坐标分别为(-1,0),(3,0),现同时将A,B两点向右平移1个单位,再向上平移2个单位,分别得到点A,B的对应点C,D,连接AC,BD,CD.
(1)求点C,D的坐标;
(2)若点P在直线BD上运动,连接PC,PO.
①若点P在线段BD上(不与B,D重合)时,求S△CDP+S△BOP的取值范围;
②若点P在直线BD上运动,试探索∠CPO,∠DCP,∠BOP的关系,并证明你的结论.
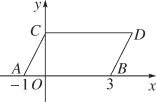
【答案】(1)由平移可知点C的坐标为(0,2),点D的坐标为(4,2);(2)①3<S△CDP+S△BOP<4;②当点![]() 在线段
在线段![]() 上时,
上时,![]() ;当点
;当点![]() 在线段
在线段![]() 的延长线上时,
的延长线上时,![]() ;当点
;当点![]() 在线段
在线段![]() 的延长线上时,
的延长线上时,![]() .
.
【解析】
(1)根据向右平移横坐标加,向上平移纵坐标加求出![]() 、
、![]() 的坐标即可;
的坐标即可;
(2)①设点![]() 的纵坐标为
的纵坐标为![]() ,将
,将![]() 与
与![]() 的面积表示出来,从而得到
的面积表示出来,从而得到![]() ,根据题可知
,根据题可知![]() ,即可得到
,即可得到![]() 的范围;
的范围;
②分三种情况,根据平移的性质可得![]() ,再过点
,再过点![]() 作
作![]() ,根据平行公理可得
,根据平行公理可得![]() ,然后根据两直线平行,内错角相等可得
,然后根据两直线平行,内错角相等可得![]() ,
,![]() 即可得到结论.
即可得到结论.
(1)由平移可知点![]() 的坐标为
的坐标为![]() ,点
,点![]() 的坐标为
的坐标为![]() ;
;
(2)①设点![]() 的纵坐标为
的纵坐标为![]() ,
,
![]() 点
点![]() 在线段
在线段![]() 上运动,点
上运动,点![]() 、
、![]() 的坐标分别为
的坐标分别为![]() ,
,![]() ,易知
,易知![]() ,
,![]() ,
,![]() ,
,![]() 轴,
轴,
![]()
![]() ,
,![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() ;
;
②当点![]() 在线段
在线段![]() 上时,如图1
上时,如图1
由平移的性质得,![]() ,
,
过点![]() 作
作![]() ,则
,则![]() ,
,
![]() ,
,![]() ,
,
![]() ,
,
当点![]() 在线段
在线段![]() 的延长线上时,如图2,
的延长线上时,如图2,
由平移的性质得,![]() ,
,
点![]() 作
作![]() ,则
,则![]() ,
,
![]() ,
,![]() ,
,
![]() ,
,
当点![]() 在线段
在线段![]() 的延长线上时,如图3,
的延长线上时,如图3,
同(2)的方法得出![]() .
.





科目:初中数学 来源: 题型:
【题目】经过某十字路口的汽车,它可能继续直行,也可能向左转或向右转,如果这三种情况是等可能的,当三辆汽车经过这个十字路口时:
(1)请你用列表或画树状图的方法,表示出所有可能的结果;
(2)三辆车全部同向而行的概率是 ,至少有两辆车向左转的概率是 ;
(3)由于十字路口右拐弯处是通往新建经济开发区的,因此交管部门在汽车行驶高峰时段对车流量作了统计,发现汽车在此十字路口向右转的频率为![]() ,向左转和直行的频率均为
,向左转和直行的频率均为![]() .目前在此路口,汽车左转、右转、直行的绿灯亮的时间分别为30秒,在绿灯亮总时间不变的条件下,为了缓解交通拥挤,请你用统计的知识对此路口三个方向的绿灯亮的时间做出合理的调整.
.目前在此路口,汽车左转、右转、直行的绿灯亮的时间分别为30秒,在绿灯亮总时间不变的条件下,为了缓解交通拥挤,请你用统计的知识对此路口三个方向的绿灯亮的时间做出合理的调整.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系xOy中,点A(1,1),B(3,2),将点A向左平移两个单位,再向上平移4个单位得到点C.
(1)写出点C坐标;
(2)求△ABC的面积.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,在平面直角坐标系中,![]() ,过C作
,过C作![]() 轴于B.
轴于B.
(1)三角形ABC的面积![]() _____________;
_____________;
(2)如图2,过B作![]() 交y轴于D,且AE,DE分别平分∠CAB,∠ODB,求∠AED的度数;
交y轴于D,且AE,DE分别平分∠CAB,∠ODB,求∠AED的度数;
(3)点P在y轴上,使得三角形ABC和三角形ACP的面积相等,直接写出P点坐标.



查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了预防疾病,某单位对办公室采用药熏消毒法进行消毒,已知药物燃烧时,室内每立方米空气中的含药量y(毫克)与时间x(分钟)成为正比例,药物燃烧后,y与x成反比例(如图),现测得药物8分钟燃毕,此时室内空气中每立方米的含药量6毫克,请根据题中所提供的信息,解答下列问题:

(1)药物燃烧时,y关于x的函数关系式为________,自变量x的取值范为________;药物燃烧后,y关于x的函数关系式为________.
(2)研究表明,当空气中每立方米的含药量低于1.6毫克时员工方可进办公室,那么从消毒开始,至少需要经过________分钟后,员工才能回到办公室;
(3)研究表明,当空气中每立方米的含药量不低于3毫克且持续时间不低于10分钟时,才能有效杀灭空气中的病菌,那么此次消毒是否有效?为什么?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,将矩形纸片ABCD(如图①)按如下步骤操作:(1)以过点A的直线为折痕折叠纸片,使点B恰好落在AD边上,折痕与BC边交于点E(如图②);(2)以过点E的直线为折痕折叠纸片,使点A落在BC边上,折痕EF交AD边于点F(如图③);(3)将纸片展平,那么∠AFE的度数为_________.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某家电销售商城电冰箱的销售价为每台2100元,空调的销售价为每台1750元,每台电冰箱的进价比每台空调的进价多400元,商城用80000元购进电冰箱的数量与用64000元购进空调的数量相等.
(1)求每台电冰箱与空调的进价分别是多少;
(2)现在商城准备一次购进这两种家电共100台,设购进电冰箱x台,这100台家电的销售总利润为y元,要求购进空调数量不超过电冰箱数量的2倍,总利润不低于13000元,请分析合理的方案共有多少种,并确定获利最大的方案以及最大利润;
(3)实际进货时,厂家对电冰箱出厂价下调k(0<k<100)元,若商店保持这两种家电的售价不变,请你根据以上信息及(2)问中条件,设计出使这100台家电销售总利润最大的进货方案.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com