
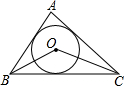
 如图,⊙O是△ABC的内切圆,若∠ABC=70°,∠ACB=40°,则∠BOC=125°.
如图,⊙O是△ABC的内切圆,若∠ABC=70°,∠ACB=40°,则∠BOC=125°. 分析 根据三角形内心的性质得到OB平分∠ABC,OC平分∠ACB,根据角平分线定义得∠OBC=$\frac{1}{2}$∠ABC=35°,∠OCB=$\frac{1}{2}$∠ACB=20°,然后根据三角形内角和定理计算∠BOC.
解答 解:∵⊙O是△ABC的内切圆,
∴OB平分∠ABC,OC平分∠ACB,
∴∠OBC=$\frac{1}{2}$∠ABC=35°,∠OCB=$\frac{1}{2}$∠ACB=20°,
∴∠BOC=180°-∠OBC-∠OCB=180°-35°-20°=125°.
故答案为125.
点评 本题考查了三角形的内切圆与内心:与三角形各边都相切的圆叫三角形的内切圆,三角形的内切圆的圆心叫做三角形的内心,这个三角形叫做圆的外切三角形.三角形的内心就是三角形三个内角角平分线的交点.


科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 某公司招聘人才,对应聘者分别进行阅读能力、思维能力和表达能力三项测试,其中甲、乙两人的成绩如表(单位:分):
某公司招聘人才,对应聘者分别进行阅读能力、思维能力和表达能力三项测试,其中甲、乙两人的成绩如表(单位:分):| 项目人员 | 阅读能力 | 思维能力 | 表达能力 |
| 甲 | 93 | 86 | 73 |
| 乙 | 95 | 81 | 79 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| 周一 | 周二 | 周三 | 周四 | 周五 | 周六 | 周日 |
| 26 | 36 | 22 | 22 | 24 | 31 | 21 |
| A. | 中位数是22 | B. | 平均数是26 | C. | 众数是22 | D. | 极差是15 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com