【题目】（1）先化简，再求值：（a+
）÷（
﹣a+2），请从﹣1，0，1中选取一个作为a的值代入求值．
（2）解方程：
﹣1＝
【答案】（1）取a＝0，则原式＝1；（2）原方程无解．
【解析】
（1）首先对括号内的分式通分相加，然后转化为乘法计算，即可化简，然后选取一个能使分式有意义的a的值代入求解．
（2）观察可得最简公分母是（x+2）（x-2），方程两边乘最简公分母，可以把分式方程转化为整式方程求解，结果要检验．
解：（1）（a+
）÷（
﹣a+2）
＝（
+）÷（﹣
）
＝
÷
＝
＝
，
∵a=±1时，原式无意义，
∴取a＝0，
则原式＝1；
（2）方程两边都乘以（x+2）（x﹣2），得：x（x+2）﹣（x+2）（x﹣2）＝8，
化简，得：2x+4=8 ,
解得：x＝2，
检验，将x＝2代入（x+2）（x﹣2）＝0，
所以，x＝2 是原方程的增根，
原方程无解．
故答案为：（1）取a＝0，则原式＝1；（2）原方程无解．
举一反三单元同步过关卷系列答案科目：初中数学 来源： 题型：
【题目】某部队将在指定山区进行军事演习，为了使道路便于部队重型车辆通过，部队工兵连接到抢修一段长3600米道路的任务，按原计划完成总任务的
后，为了让道路尽快投入使用，工兵连将工作效率提高了50%，一共用了10小时完成任务．
（1）按原计划完成总任务的
时，已抢修道路 米；
（2）求原计划每小时抢修道路多少米？
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图是某航空公司托运行李的费用y(元)与行李的质量x(千克)之间的关系，由图可以看出：
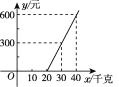
(1)当行李质量为30千克时，行李托运费是________元；
(2)当行李质量为________千克时，行李托运费是600元；
(3)每位旅客最多可以免费携带________千克的行李．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图，点 E 在 AD 的延长线上，下列条件中能判断 AB∥CD 的是（ ）
A. ∠1=∠4B. ∠2=∠3C. ∠C=∠CDED. ∠C+∠CDA=180°
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图，∠AEM＝∠DFN＝a，∠EMN＝∠MNF＝b，∠PEM＝
∠AEM，∠MNP＝∠FNP，∠BEP，∠NFD的角平分线交于点I，若∠I＝∠P，则a和b的数量关系为_____（用含a的式子表示b）．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图，CD⊥AB于D，点E为AC上一动点，过点E作EF⊥AB于F，连接DE．
（1）若∠1＝∠2，求证：DE∥BC；
（2）在点E运动过程中，直线DE与直线BC交于点M，若∠DCB＝α，∠M＝β，则∠FED的度为 （用含α，β的式子表示）．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】平面直角坐标系中，点A坐标为（a，0），点B坐标为（b，2），点C坐标为（c，m），其中a、b、c满足方程组
．
（1）若a＝2，则三角形AOB的面积为 ；
（2）若点B到y轴的距离是点C到y轴距离的2倍，求a的值；
（3）连接AB、AC、BC，若三角形ABC的面积小于等于9，求m的取值范围．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】在一个不透明的袋子中装有红、黑、白三种球共
个，他们除了颜色外其余完全一样． 已知黑球是白球的
倍少
个，将球充分搅匀后，随机摸出一球是红球的概率是
（1）这三种球各有多少个？
（2）随机摸出一球是白球的概率是多少？
（3）若从袋子中拿出
个球(没有红球)后，随机摸一次摸到红球的概率是多少？
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图，是屋架设计图的一部分，点D是斜梁AB的中点，立柱BC、DE垂直于横梁AC，AB=4m，∠A=30°，则DE等于（ ）
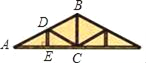
A. 1m B. 2m C. 3m D. 4m
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com