
【题目】直接写出计算结果:
(1) -2-11 = (2) 5-(-12)=
(3) (-5)×(-6) = (4) ![]()
(5)![]() = (6)
= (6) ![]() =
=
(7)-3.5+3.5 = (8)![]() =
=
 提分百分百检测卷系列答案
提分百分百检测卷系列答案 宝贝计划期末冲刺夺100分系列答案
宝贝计划期末冲刺夺100分系列答案 能考试全能100分系列答案
能考试全能100分系列答案科目:初中数学 来源: 题型:
【题目】小丽暑假期间参加社会实践活动,从某批发市场以批发价每个![]() 元的价格购进
元的价格购进![]() 个手机充电宝,然后每个加价
个手机充电宝,然后每个加价![]() 元到市场出售.
元到市场出售.
![]() 求售出
求售出![]() 个手机充电宝的总售价为多少元(结果用含
个手机充电宝的总售价为多少元(结果用含![]() ,
,![]() 的式子表示)?
的式子表示)?
![]() 由于开学临近,小丽在成功售出
由于开学临近,小丽在成功售出![]() 个充电宝后,决定将剩余充电宝按售价
个充电宝后,决定将剩余充电宝按售价![]() 折出售,并很快全部售完.
折出售,并很快全部售完.
①相比不采取降价销售,她将比实际销售多盈利多少元(结果用含![]() 、
、![]() 的式子表示)?
的式子表示)?
②若![]() ,小丽实际销售完这批充电宝的利润率为________(利润率
,小丽实际销售完这批充电宝的利润率为________(利润率![]() 利润
利润![]() 进价
进价![]() )
)
查看答案和解析>>
科目:初中数学 来源: 题型:
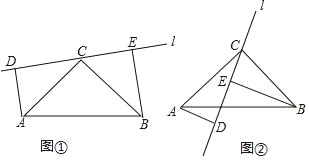
【题目】探究:如图①,在Rt△ABC中,∠ACB=90°,AC=BC,直线l经过点C,且点A、B在直线l的同侧,过点A、B分别作直线l的垂线,垂足分别为点D、E.求证:DE=AD+BE.
应用:如图②,在Rt△ABC中,∠ACB=90°,AC=BC,直线l经过点C,且点A、B在直线l的异侧,过点A、B分别作直线l的垂线,垂足分别为点D、E.直接写出线段AD、BE、DE之间的相等关系.
查看答案和解析>>
科目:初中数学 来源: 题型:
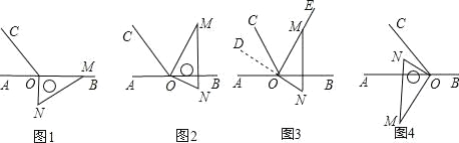
【题目】已知,在下列各图中,点 O 为直线 AB 上一点,∠AOC=60°,直角三角板的直角顶点放在点处.
(1)如图 1,三角板一边 OM在射线 OB 上,另一边 ON在直线 AB的下方,求∠BOC的度数,∠CON 的度数;
(2)如图 2,三角板一边OM恰好在∠BOC的角平分线OE上,另一边ON在直线 AB的下方,求此时∠BON 的度数;
(3)请从下列(A),(B)两题中任选一题作答. 我选择哪一题.
(A)在图 2 中,延长线段 NO 得到射线 OD,如图 3,求∠AOD 的度数;写出∠DOC 与∠BON 的数量关系;
(B)如图 4,MN⊥AB,ON 在∠AOC 的内部,若另一边 OM 在直线 AB 的下方, 求∠COM+∠AON 的度数;∠AOM﹣∠CON 的度数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知二次函数的图象经过A(2,0)、C(0,12)两点,且对称轴为直线x=4.设顶点为点P,与x轴的另一交点为点B.
(1)求二次函数的解析式及顶点P的坐标;
(2)如图1,在直线 y=2x上是否存在点D,使四边形OPBD为等腰梯形?若存在,求出点D的坐标;若不存在,请说明理由;
(3)如图2,点M是线段OP上的一个动点(O、P两点除外),以每秒 ![]() 个单位长度的速度由点P向点O 运动,过点M作直线MN∥x轴,交PB于点N.将△PMN沿直线MN对折,得到△P1MN.在动点M的运动过程中,设△P1MN与梯形OMNB的重叠部分的面积为S,运动时间为t秒.求S关于t的函数关系式.
个单位长度的速度由点P向点O 运动,过点M作直线MN∥x轴,交PB于点N.将△PMN沿直线MN对折,得到△P1MN.在动点M的运动过程中,设△P1MN与梯形OMNB的重叠部分的面积为S,运动时间为t秒.求S关于t的函数关系式.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,两个等腰直角△ABC和△CDE中,∠ACB=∠DCE=90°.
(1)观察猜想如图1,点E在BC上,线段AE与BD的数量关系,位置关系.
(2)探究证明把△CDE绕直角顶点C旋转到图2的位置,(1)中的结论还成立吗?说明理由;
(3)拓展延伸:把△CDE绕点C在平面内自由旋转,若AC=BC=13,DE=10,当A、E、D三点在直线上时,请直接写出AD的长.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知直线l1∥l2,直线l3和直线l1,l2分别交于点C和D,点P在直线l3上.
(1)若点P在C,D两点之间运动,∠PAC,∠APB,∠PBD之间的关系是否发生变化?若变化,请说明理由;若不变,请求出它们之间的关系式.
(2)若点P在C,D两点的外侧运动(点P与点C,D不重合),则∠PAC,∠APB,∠PBD之间的关系又如何?

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,O是坐标原点,点A的坐标是(﹣2,4),过点A作AB⊥y轴,垂足为B,连接OA.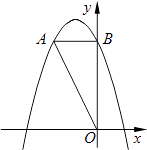
(1)求△OAB的面积;
(2)若抛物线y=﹣x2﹣2x+c经过点A.
①求c的值;
②将抛物线向下平移m个单位,使平移后得到的抛物线顶点落在△OAB的内部(不包括△OAB的边界),求m的取值范围(直接写出答案即可).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,分别以点A和点B为圆心,大于 ![]() AB的长为半径画弧,两弧相交于点M,N,作直线MN,交BC于点D,连接AD.若△ADC的周长为10,AB=7,则△ABC的周长为( )
AB的长为半径画弧,两弧相交于点M,N,作直线MN,交BC于点D,连接AD.若△ADC的周长为10,AB=7,则△ABC的周长为( ) 
A.7
B.14
C.17
D.20
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com