
��ͼ��ֱ��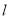 ��
��  ��
��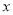 �ᡢ
�ᡢ ��ֱ��ڵ�B��C������B��C�����������
��ֱ��ڵ�B��C������B��C����������� ��
�� �����һ������ΪA��
�����һ������ΪA��
��1����������ߵĽ���ʽ��
��2������P��ֱ�� �·����������ϣ�����P��PD��
�·����������ϣ�����P��PD�� �ύ
�ύ �ڵ�D��PE��
�ڵ�D��PE�� �ύ
�ύ �ڵ�E��
�ڵ�E��
��PD+PE�����ֵ��
��3����FΪֱ�� �ϵĵ㣬��A��B��P��FΪ������ı����ܷ�ƽ���ı��Σ����ܣ������F�����ꣻ�����ܣ���˵�����ɣ�
�ϵĵ㣬��A��B��P��FΪ������ı����ܷ�ƽ���ı��Σ����ܣ������F�����ꣻ�����ܣ���˵�����ɣ�

 ��ʦ����ɳ���ʱͬ��ѧ����ϵ�д�
��ʦ����ɳ���ʱͬ��ѧ����ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ��2017-2018ѧ�������ʡ�����жŶ������ؾ��꼶���ϣ���ĩ��ѧ�Ծ�������ѧ�ƣ� ���ͣ������
��ͼ����ֱ֪��y=��2x+12�ֱ���y�ᣬx�ύ��A��B���㣬��M��y���ϣ��Ե�MΪԲ�ĵġ�M��ֱ��AB�����ڵ�D������MD��
��1����֤����ADM�ס�AOB��
��2�������M�İ뾶Ϊ2 ����д����M�����꣬��д���ԣ���
����д����M�����꣬��д���ԣ��� ��
��  ��Ϊ���㣬�ҹ���M�������ߵĽ���ʽ��
��Ϊ���㣬�ҹ���M�������ߵĽ���ʽ��

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ��2017-2018ѧ�����꼶��ѧ��ʦ����ϲ��4�� ����ƽ��ͼ�� ��Ԫ���Ծ� ���ͣ���ѡ��
��ͼ����һ�ų�����ֽƬ���ۣ�Ȼ�����һ���ǣ���������Ľ�չ������һ��ֱ�ǣ���ô���������ۺ�AB�γɵļнǶ�����(����)

A. 180�� B. 90�� C. 45�� D. 22.5��
C ����������������������۵�ͼ�ε����ʿ�֪�����������ۺ�AB�γɵļнǵĶ���=90���2=45�㣬��ѡ��C���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ��ɽ��ʡ���ݵ���2017-2018ѧ��ȵ�һѧ����ĩ�����꼶��ѧ�Ծ� ���ͣ���ѡ��
��ͼ,��֪��ABE�ա�ACD,����ѡ���в��ܱ�֤���ĵ�ʽ��( )

A. AD=AE B. DB=AE C. DF=EF D. DB=EC
B ������������������ߡ�ABE�ա�ACD�� ��AB=AC��AD=AE����B=��C����A��ȷ�� ��AB-AD=AC-AE����BD=EC����D��ȷ�� �ڡ�BDF�͡�CEF�� ���BDF�ա�CEF��ASA���� ��DF=EF����C��ȷ�� ��ѡB���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ��ɽ��ʡ���ݵ���2017-2018ѧ��ȵ�һѧ����ĩ�����꼶��ѧ�Ծ� ���ͣ���ѡ��
����ʽ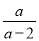 ������,��a��ȡֵ��Χ��( )
������,��a��ȡֵ��Χ��( )
A. a��2 B. a��0 C. a��2��a��0 D. һ��ʵ��
A �������������������������ã�a-2��0�� ��ã�a��2�� ��ѡA���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ���㶫ʡ��ͷ�гκ���2018����꼶��ѧ����ĩ���������ѧ�Ծ� ���ͣ������
����������������շ�վʱ��4���շ�ͨ�� A��B��C��D�У������ѡ�����е�һ��ͨ����
��1��һ�����������շ�վʱ��ѡ�� Aͨ��ͨ���ĸ����� ��
��2�����������������շ�վʱ��ѡ��ͬͨ��ͨ���ĸ��ʣ�
��1������2���� �������������������1�����ݸ��ʹ�ʽ���ɵõ����ۣ� ��2��������״ͼ���ɵõ����ۣ� �����������1��ѡ�� Aͨ��ͨ���ĸ���=�� �ʴ�Ϊ�� �� ��2����������Ϊ�ף��ң���ͼ���������������շ�վʱ������16�ֿ��ܵĽ��������ѡ��ͬͨ��ͨ������12�ֽ������ѡ��ͬͨ��ͨ���ĸ���==���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ���㶫ʡ��ͷ�гκ���2018����꼶��ѧ����ĩ���������ѧ�Ծ� ���ͣ������
������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ��2018�˽̰���꼶��ѧ�²���ϰ����ʮ���´����� ���ͣ������
��ͼ����֪D�ǡ�ABC�ı�AB��һ�㣬CE��AB��DE��AC�ڵ�O����OA=OC�������߶�CD���߶�AE�Ĵ�С��ϵ��λ�ù�ϵ��������֤����

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ���㶫ʡ��ݸ�к���ѧУ2017-2018ѧ����꼶���ϣ�������ѧ�Ծ���word�溬�𰸽����� ���ͣ������
���㣺��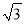 ��
�� ��2+��
��2+�� +3����
+3����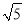 ��3����
��3����
�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com