
【题目】正方形ABCD中,点E是BD上一点,过点E作EF⊥AE交射线CB于点F,连结CE.
(1)已知点F在线段BC上.
①若AB=BE,求∠DAE度数;
②求证:CE=EF;
(2)已知正方形边长为2,且BC=2BF,请直接写出线段DE的长.

【答案】(1)①22.5°;②证明见解析;(2)![]() 或
或![]() .
.
【解析】
(1)①先求得∠ABE的度数,然后依据等腰三角形的性质和三角形内角和定理求得∠BAE的度数,然后可求得∠DAE度数;
②先利用正方形的对称性可得到∠BAE=∠BCE,然后在证明又∠BAE=∠EFC,通过等量代换可得到∠BCE=∠EFC;
(2)当点F在BC上时,过点E作MN⊥BC,垂直为N,交AD于M.依据等腰三角形的性质可得到FN=CN,从而可得到NC的长,然后可得到MD的长,在Rt△MDE中可求得ED的长;当点F在CB的延长线上时,先根据题意画出图形,然后再证明EF=EC,然后再按照上述思路进行解答即可.
(1)①∵ABCD为正方形,∴∠ABE=45°,
又∵AB=BE,∴∠BAE![]() (180°﹣45°)=67.5°,
(180°﹣45°)=67.5°,
∴∠DAE=90°﹣67.5°=22.5°;
②∵正方形ABCD关于BD对称,
∴△ABE≌△CBE,∴∠BAE=∠BCE,
又∵∠ABC=∠AEF=90°,∴∠BAE=∠EFC,∴∠BCE=∠EFC,∴CE=EF;
(2)如图1,过点E作MN⊥BC,垂直为N,交AD于M,
∵CE=EF,∴N是CF的中点,
∵BC=2BF,∴![]() ,
,
又∵四边形CDMN是矩形,△DME为等腰直角三角形,
∴CN=DM=ME,
∴ED![]() DM
DM![]() CN
CN![]() ;
;
如图2,过点E作MN⊥BC,垂直为N,交AD于M,
∵正方形ABCD关于BD对称,∴△ABE≌△CBE,∴∠BAE=∠BCE,
又∵∠ABF=∠AEF=90°,∴∠BAE=∠EFC,
∴∠BCE=∠EFC,∴CE=EF,∴FN=CN,
又∵BC=2BF,∴FC=3,∴CN![]() ,∴EN=BN
,∴EN=BN![]() ,∴DE
,∴DE![]() ,
,

综上所述:ED的长为![]() 或
或![]() .
.


 100分闯关期末冲刺系列答案
100分闯关期末冲刺系列答案科目:初中数学 来源: 题型:
【题目】在△ABC中,AB=AC=5,cos∠ABC= ![]() ,将△ABC绕点C顺时针旋转,得到△A1B1C.
,将△ABC绕点C顺时针旋转,得到△A1B1C.
(1)如图①,当点B1在线段BA延长线上时.①求证:BB1∥CA1;②求△AB1C的面积;
(2)如图②,点E是BC边的中点,点F为线段AB上的动点,在△ABC绕点C顺时针旋转过程中,点F的对应点是F1 , 求线段EF1长度的最大值与最小值的差.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】“十一”黄金周,坚胜家电城大力促销,收银情况一直看好![]() 下表为当天与前一天的营业额的涨跌情况
下表为当天与前一天的营业额的涨跌情况![]() 已知9月30日的营业额为26万元.
已知9月30日的营业额为26万元.
10月1日 | 2日 | 3日 | 4日 | 5日 | 6日 | 7日 |
4 | 3 | 2 | 0 |
|
|
|
![]() 黄金周内收入最低的哪一天?
黄金周内收入最低的哪一天?![]() 直接回答,不必写过程
直接回答,不必写过程![]() .
.
![]() 黄金周内平均每天的营业额是多少?
黄金周内平均每天的营业额是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为选拔参加八年级数学“拓展性课程”活动人选,数学李老师对本班甲、乙两名学生以前经历的10次测验成绩(分)进行了整理、分析(见图①):

(1)写出a,b的值;
(2)如要推选1名学生参加,你推荐谁?请说明你推荐的理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
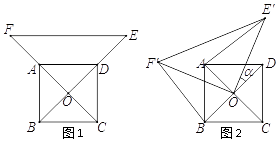
【题目】如图1,已知 ![]() 为正方形
为正方形 ![]() 的中心,分别延长
的中心,分别延长 ![]() 到点
到点 ![]() ,
, ![]() 到点
到点 ![]() ,使
,使 ![]() ,
, ![]() ,连结
,连结 ![]() ,将△
,将△ ![]() 绕点
绕点 ![]() 逆时针旋转
逆时针旋转 ![]() 角得到△
角得到△ ![]() (如图2).连结
(如图2).连结 ![]() 、
、 ![]() .
.
(Ⅰ)探究 ![]() 与
与 ![]() 的数量关系,并给予证明;
的数量关系,并给予证明;
(Ⅱ)当 ![]() ,
, ![]() 时,求:
时,求:
① ![]() 的度数;
的度数;
② ![]() 的长度.
的长度.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读材料: 小明在学习二次根式后,发现一些含根号的式子可以写成另一个式子的平方,如:![]() ,善于思考的小明进行了以下探索:
,善于思考的小明进行了以下探索:
设![]() (其中
(其中![]() 均为整数),则有
均为整数),则有![]() .
.
∴![]() .这样小明就找到了一种把部分
.这样小明就找到了一种把部分![]() 的式子化为平方式的方法.
的式子化为平方式的方法.
请你仿照小明的方法探索并解决下列问题:
当![]() 均为正整数时,若
均为正整数时,若![]() ,用含m、n的式子分别表示
,用含m、n的式子分别表示![]() ,得
,得![]() = ,
= ,![]() = ;
= ;
(2)利用所探索的结论,找一组正整数![]() ,填空: + =( +
,填空: + =( + ![]() )2;
)2;
(3)若![]() ,且
,且![]() 均为正整数,求
均为正整数,求![]() 的值.
的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】鲁能巴蜀中学2018年校艺术节“巴蜀好声音”独唱预选赛中,初二年级25名同学的成绩![]() 满分为10分
满分为10分![]() 统计如下:
统计如下:![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,10
,10
![]() 分及以上为A级,
分及以上为A级,![]() 分为B级
分为B级![]() 包括
包括![]() 分和
分和![]() 分
分![]() ,
,![]() 分为C级
分为C级![]() 包括
包括![]() 分和
分和![]() 分
分![]() ,
,![]() 分以下为D级
分以下为D级![]() 请把下面表格补充完整;
请把下面表格补充完整;
等级 | A | B | C | D |
人数 | 4 | 8 |
![]() 级8位同学成绩的中位数是多少,众数是多少;
级8位同学成绩的中位数是多少,众数是多少;
![]() 若成绩为A级的同学将参加学校的汇演,请求出初二年级A级同学的平均成绩?
若成绩为A级的同学将参加学校的汇演,请求出初二年级A级同学的平均成绩?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知反比例函数 ![]() ,则下列结论不正确的是( )
,则下列结论不正确的是( )
A.图象必经过点(-1,5)
B.图象的两个分支分布在第二、四象限
C.y随x的增大而增大
D.若x>1,则-5<y<0
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com