
ЁОЬтФПЁПФГЩЬЦЗЕФНјМлЮЊУПМў40дЊЃЌЪлМлВЛЕЭгк50дЊЃЌШчЙћЪлМлЮЊУПМў50дЊЃЌУПИідТПЩТєГі210МўЃЛШчЙћЪлМлГЌЙ§50дЊЕЋВЛГЌЙ§80дЊЃЌУПМўЩЬЦЗЕФЪлМлУПЩЯеЧ1дЊЃЌдђУПдТЩйТє1МўЃЛШчЙћЪлМлГЌЙ§80дЊКѓЃЌШєдйеЧМлЃЌдђУПеЧ1дЊУПдТЩйТє3МўЃЌЩшУПМўЩЬЦЗЕФЪлМлЮЊxдЊЃЌУПдТЕФЯњЪлСПЮЊyМўЃЎ
ЃЈ1ЃЉЧѓyгыxЕФКЏЪ§ЙиЯЕЪНВЂаДГіздБфСПxЕФШЁжЕЗЖЮЇЃЛ
ЃЈ2ЃЉУПМўЩЬЦЗЕФЪлМлЖЈЮЊЖрЩйдЊЪБЃЌУПИідТПЩЛёЕУзюДѓРћШѓЃПзюДѓЕФдТРћШѓЪЧЖрЩйдЊЃП
ЁОД№АИЁП(1)Ѓљ=![]() (2) 7500дЊ
(2) 7500дЊ
ЁОНтЮіЁПЗжЮіЃКЃЈ1ЃЉЕБЪлМлГЌЙ§50дЊЕЋВЛГЌЙ§80дЊЃЌУПМўЩЬЦЗЕФЪлМлУПЩЯеЧ1дЊЃЌдђУПИідТЩйТє1МўЃЌy=260-xЃЌ50ЁмxЁм80ЃЌЕБШчЙћЪлМлГЌЙ§80дЊКѓЃЌШєдйеЧМлЃЌдђУПеЧ1дЊУПдТЩйТє3МўЃЌy=420-3xЃЌ80ЃМxЃМ140ЃЌ
ЃЈ2ЃЉгЩРћШѓ=ЃЈЪлМл-ГЩБОЃЉЁСЯњЪлСПСаГіКЏЪ§ЙиЯЕЪНЃЌНЋНтЮіЪНХфЗНГЩЖЅЕуЪНКѓРћгУЖўДЮКЏЪ§ЕФаджЪЧѓНтПЩЕУЃЎ
ЯъНтЃКЃЈ1ЃЉЕБ50ЁмxЁм80ЪБЃЌy=210ЉЃЈxЉ50ЃЉЃЌМДy=260ЉxЃЌ
ЕБ80ЃМxЃМ140ЪБЃЌy=210ЉЃЈ80Љ50ЃЉЉ3ЃЈxЉ80ЃЉЃЌМДy=420Љ3xЃЎ
дђy=![]() ЃЛ
ЃЛ
ЃЈ2ЃЉЕБ50ЁмxЁм80ЪБЃЌw=Љx2+300xЉ10400=ЉЃЈxЉ150ЃЉ2+12100ЃЌ
ЕБxЃМ150ЪБЃЌwЫцxдіДѓЖјдіДѓЃЌ
дђЕБx=80ЪБЃЌwзюДѓ=7200ЃЛ
ЕБ80ЃМxЁм140ЪБЃЌw=Љ3x2+540xЉ16800=Љ3ЃЈxЉ90ЃЉ2+7500ЃЌ
ЕБx=90ЪБЃЌwзюДѓ=7500ЃЌ
Ёрx=90ЪБЃЌWгазюДѓжЕ7500дЊЃЌ
Д№ЃКУПМўЩЬЦЗЕФЪлМлЖЈЮЊ90дЊЪБЃЌУПИідТПЩЛёЕУзюДѓРћШѓЪЧ7500дЊ



| ФъМЖ | ИпжаПЮГЬ | ФъМЖ | ГѕжаПЮГЬ |
| ИпвЛ | ИпвЛУтЗбПЮГЬЭЦМіЃЁ | ГѕвЛ | ГѕвЛУтЗбПЮГЬЭЦМіЃЁ |
| ИпЖў | ИпЖўУтЗбПЮГЬЭЦМіЃЁ | ГѕЖў | ГѕЖўУтЗбПЮГЬЭЦМіЃЁ |
| ИпШ§ | ИпШ§УтЗбПЮГЬЭЦМіЃЁ | ГѕШ§ | ГѕШ§УтЗбПЮГЬЭЦМіЃЁ |
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПдкЦНУцжБНЧзјБъЯЕжаЃЌжБЯпy=Љ![]() x+1НЛyжсгкЕуBЃЌНЛxжсгкЕуAЃЌХзЮяЯпy=Љ
x+1НЛyжсгкЕуBЃЌНЛxжсгкЕуAЃЌХзЮяЯпy=Љ![]() x2+bx+cОЙ§ЕуBЃЌгыжБЯпy=Љ
x2+bx+cОЙ§ЕуBЃЌгыжБЯпy=Љ![]() x+1НЛгкЕуCЃЈ4ЃЌЉ2ЃЉЃЎ
x+1НЛгкЕуCЃЈ4ЃЌЉ2ЃЉЃЎ
ЃЈ1ЃЉЧѓХзЮяЯпЕФНтЮіЪНЃЛ
ЃЈ2ЃЉШчЭМЃЌКсзјБъЮЊmЕФЕуMдкжБЯпBCЩЯЗНЕФХзЮяЯпЩЯЃЌЙ§ЕуMзїMEЁЮyжсНЛжБЯпBCгкЕуEЃЌвдMEЮЊжБОЖЕФдВНЛжБЯпBCгкСэвЛЕуDЃЌЕБЕуEдкxжсЩЯЪБЃЌЧѓЁїDEMЕФжмГЄЃЎ
ЃЈ3ЃЉНЋЁїAOBШЦзјБъЦНУцФкЕФФГвЛЕуАДЫГЪБеыЗНЯђа§зЊ90ЁуЃЌЕУЕНЁїA1O1B1ЃЌЕуAЃЌOЃЌBЕФЖдгІЕуЗжБ№ЪЧЕуA1ЃЌO1ЃЌB1ЃЌШєЁїA1O1B1ЕФСНИіЖЅЕуЧЁКУТфдкХзЮяЯпЩЯЃЌЧыжБНгаДГіЕуA1ЕФзјБъЃЎ

ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
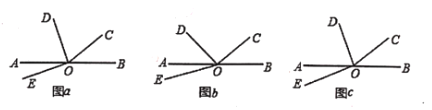
ЁОЬтФПЁПШчЭМЃЌOЮЊжБЯпABЩЯвЛЕуЃЌЁЯBOCЃН36Ёу.
ЃЈ1)ШєODЦНЗжЁЯAOCЃЌЁЯDOEЃН90ЁуЃЌШчЭМЃЈa)ЫљЪОЃЌЧѓЁЯAOEЕФЖШЪ§ЃК
ЃЈ2)ШєЁЯAODЃН![]() ЁЯAOCЃЌЁЯDOEЃН60ЁуЃЌШчЭМ(bЃЉЫљЪОЃЌЧѓЁЯAOEЕФЖШЪ§ЃК
ЁЯAOCЃЌЁЯDOEЃН60ЁуЃЌШчЭМ(bЃЉЫљЪОЃЌЧѓЁЯAOEЕФЖШЪ§ЃК
ЃЈ3ЃЉШєЁЯAODЃН![]() ЁЯAOCЃЌЁЯDOEЃН
ЁЯAOCЃЌЁЯDOEЃН![]() (nЁн2ЃЌЧвnЮЊе§ећЪ§)ЃЌШчЭМ(c)ЫљЪОЃЌЧыгУnКЌЕФДњЪ§ЪНБэЪОЁЯAOEЕФЖШЪ§__________(жБНгаДГіНсЙћ).
(nЁн2ЃЌЧвnЮЊе§ећЪ§)ЃЌШчЭМ(c)ЫљЪОЃЌЧыгУnКЌЕФДњЪ§ЪНБэЪОЁЯAOEЕФЖШЪ§__________(жБНгаДГіНсЙћ).
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЃЌABCDЪЧжБНЧЬнаЮЃЌAB=18cmЃЌCD=15cmЃЌAD=6cmЃЌЕуPДгBЕуПЊЪМЃЌбиBAБпЯђЕуAвд1cm/sЕФЫйЖШвЦЖЏЃЌЕуQДгDЕуПЊЪМЃЌбиDCБпЯђЕуCвд2cm/sЕФЫйЖШвЦЖЏЃЌШчЙћPЁЂQЗжБ№ДгBЁЂDЭЌЪБГіЗЂЃЌPЁЂQгавЛЕуЕНДяжеЕуЪБдЫЖЏЭЃжЙЃЌЩшвЦЖЏЪБМфЮЊtЃЎ
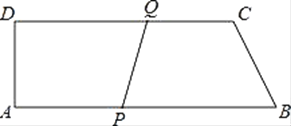
ЃЈ1ЃЉtЮЊКЮжЕЪБЫФБпаЮPQCBЪЧЦНааЫФБпаЮЃП
ЃЈ2ЃЉtЮЊКЮжЕЪБЫФБпаЮPQCBЪЧОиаЮЃП
ЃЈ3ЃЉtЮЊКЮжЕЪБЫФБпаЮPQCBЪЧЕШбќЬнаЮЃП
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
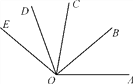
ЁОЬтФПЁПШчЭМЃЌOBЮЊЁЯAOCЕФЦНЗжЯпЃЌODЪЧЁЯCOEЕФЦНЗжЯпЃЎ
(1)ШчЙћЁЯAOBЃН40ЁуЃЌЁЯDOEЃН30ЁуЃЌФЧУДЁЯBODЮЊЖрЩйЖШЃП
(2)ШчЙћЁЯAOEЃН140ЁуЃЌЁЯCODЃН30ЁуЃЌФЧУДЁЯAOBЮЊЖрЩйЖШЃП
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПЧыИљОнЭМжаЬсЙЉЕФаХЯЂЃЌЛиД№ЯТСаЮЪЬтЁЃ
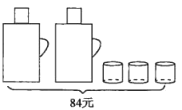
ЃЈ1ЃЉвЛИіХЏЦПгывЛИіЫЎБЗжБ№ЪЧЖрЩйдЊЃП
ЃЈ2ЃЉМзЁЂввСНМвЩЬГЁЭЌЪБГіЪлЭЌбљЕФХЏЦПКЭЫЎБЃЌЮЊСЫгНгаТФъЃЌСНМвЩЬГЁЖМдкИуДйЯњЛюЖЏЃЌМзЩЬГЁЙцЖЈЃКетСНжжЩЬЦЗЖМДђОХелЃЛввЩЬГЁЙцЖЈЃКТђвЛИіХЏЦПдљЫЭвЛИіЫЎБ.ШєФГЕЅЮЛЯывЊТђ4ИіХЏЦПКЭ15ИіЫЎБЃЌЧыЮЪбЁдёФФМвЩЬГЁЙКТђИќКЯЫуЃЌВЂЫЕУїРэгЩ.
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЃЌОиаЮABCDЕФБпAB=3cmЃЌAD=4cmЃЌЕуEДгЕуAГіЗЂЃЌбиЩфЯпADвЦЖЏЃЌвдCEЮЊжБОЖзїдВOЃЌЕуFЮЊдВOгыЩфЯпBDЕФЙЋЙВЕуЃЌСЌНгEFЁЂCFЃЌЙ§ЕуEзїEGЁЭEFЃЌEGгыдВOЯрНЛгкЕуGЃЌСЌНгCGЃЎ
ЃЈ1ЃЉЪдЫЕУїЫФБпаЮEFCGЪЧОиаЮЃЛ
ЃЈ2ЃЉЕБдВOгыЩфЯпBDЯрЧаЪБЃЌЕуEЭЃжЙвЦЖЏЃЌдкЕуEвЦЖЏЕФЙ§ГЬжаЃЌ
ЂйОиаЮEFCGЕФУцЛ§ЪЧЗёДцдкзюДѓжЕЛђзюаЁжЕЃПШєДцдкЃЌЧѓГіетИізюДѓжЕЛђзюаЁжЕЃЛШєВЛДцдкЃЌЫЕУїРэгЩЃЛ
ЂкЧѓЕуGвЦЖЏТЗЯпЕФГЄЃЎ

ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
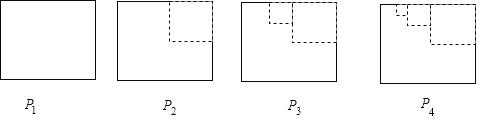
ЁОЬтФПЁПШчЭМЃЌP1ЪЧвЛПщБпГЄЮЊ1ЕФе§ЗНаЮжНАхЃЌдкP1ЕФгвЩЯЖЫМєШЅвЛИіБпГЄЮЊ![]() ЕФе§ЗНаЮКѓЕУЕНЭМаЮP2ЃЌШЛКѓвРДЮМєШЅвЛИіИќаЁЕФе§ЗНаЮЃЈЦфБпГЄЮЊЧАвЛИіБЛМєШЅЕФе§ЗНаЮБпГЄЕФвЛАыЃЉЕУЕНЭМаЮP3ЁЂP4ЁЂP5ЁЃЌМЧжНАхPnЕФУцЛ§ЮЊSnЃЌдђSnЉSn+1ЕФжЕЮЊЃЈЁЁЁЁЃЉ
ЕФе§ЗНаЮКѓЕУЕНЭМаЮP2ЃЌШЛКѓвРДЮМєШЅвЛИіИќаЁЕФе§ЗНаЮЃЈЦфБпГЄЮЊЧАвЛИіБЛМєШЅЕФе§ЗНаЮБпГЄЕФвЛАыЃЉЕУЕНЭМаЮP3ЁЂP4ЁЂP5ЁЃЌМЧжНАхPnЕФУцЛ§ЮЊSnЃЌдђSnЉSn+1ЕФжЕЮЊЃЈЁЁЁЁЃЉ
A.ЃЈ![]() ЃЉnB.ЃЈ
ЃЉnB.ЃЈ![]() ЃЉnC.ЃЈ
ЃЉnC.ЃЈ![]() ЃЉn+1D.ЃЈ
ЃЉn+1D.ЃЈ![]() ЃЉ2nЉ1
ЃЉ2nЉ1
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПдФЖСЯТСаВФСЯ
ЁАвЛДјвЛТЗЁБНЈЩшНЋвдеўВпЙЕЭЈЁЂЩшЪЉСЊЭЈЁЂУГвзГЉЭЈЁЂзЪН№ШкЭЈЁЂУёаФЯрЭЈЮЊжївЊФкШнЃЌЮЊбиЯпЙњМвЗЂеЙКЭЪРНчОМУзЂШыаТЖЏСІЃЎжаЙњгыЁАвЛДјвЛТЗЁБбиЯпЙњМвКЯзїОпгаНЯКУЕФЛљДЁ.2012ФъжаЙњгыбиЯпЙњМвЕФЛѕЮяУГвзЖюеМжаЙњЛѕЮяУГвззмЖюЕФ24.8%ЃЌ2013ФъжаЙњгыбиЯпЙњМвЕФЛѕЮяУГвзЖюеМжаЙњЛѕЮяУГвззмЖюЕФ25.0%ЃЎЫцзХЁАвЛДјвЛТЗЁБеНТдЕФЪЕЪЉЃЌжаЙњгыЁАвЛДјвЛТЗЁБбиЯпЙњМвЕФУГвзЙцФЃВЛЖЯРЉДѓЃЌ2014ФъЃЌжаЙњгыбиЯпЙњМвЕФЛѕЮяУГвзЖюДяЕН1.12ЭђвкУРдЊЃЌеМжаЙњЛѕЮяУГвззмЖюЕФ26.1%.2015ФъЃЌжаЙњгыбиЯпЙњМвЕФЛѕЮяУГвзЖюДяЕН0.93ЭђвкУРдЊЃЌеМжаЙњЛѕЮяУГвззмЖюЕФ25.3%.2016ФъЃЌжаЙњгыбиЯпЙњМвУГвзЖюЮЊ0.95ЭђвкУРдЊЃЌеМжаЙњЛѕЮяУГвззмЖюЕФ25.7%ЃЎЁАвЛДјвЛТЗЁБНЈЩшЮЊЮвУЧДђПЊСЫаТЫМТЗЃЌЪРНчЦкД§ЃЌЮЊДйНјЪРНчОМУдіГЄЁЂЩюЛЏЕиЧјКЯзїДђдьИќМсЪЕЕФЗЂеЙЛљДЁЃЌИќКУЕидьИЃСЫИїЙњШЫУёЃЎ
ИљОнвдЩЯВФСЯНтД№ЯТСаЮЪЬтЃК
ЃЈ1ЃЉЧыФугУЭГМЦЭМНЋ2012Љ2016ФъжаЙњгыЁАвЛДјвЛТЗЁБбиЯпЙњМвЕФЛѕЮяУГвзЖюеМжаЙњЛѕЮяУГвззмЖюЕФАйЗжБШБэЪОГіРДЃЌВЂдкЭМжаБъУїЯргІЪ§ОнЃЛ
ЃЈ2ЃЉИљОнВФСЯдЄЙР2017ФъжаЙњгыЁАвЛДјвЛТЗЁБбиЯпЙњМвУГвзЖюдМЮЊЁЁ ЁЁЭђвкУРдЊЃЌФуЙРМЦЕФРэгЩЪЧЁЁ ЁЁЃЎ
ВщПДД№АИКЭНтЮі>>
АйЖШжТаХ - СЗЯАВсСаБэ - ЪдЬтСаБэ
КўББЪЁЛЅСЊЭјЮЅЗЈКЭВЛСМаХЯЂОйБЈЦНЬЈ | ЭјЩЯгаКІаХЯЂОйБЈзЈЧј | ЕчаХеЉЦОйБЈзЈЧј | ЩцРњЪЗащЮожївхгаКІаХЯЂОйБЈзЈЧј | ЩцЦѓЧжШЈОйБЈзЈЧј
ЮЅЗЈКЭВЛСМаХЯЂОйБЈЕчЛАЃК027-86699610 ОйБЈгЪЯфЃК58377363@163.com