
分析 (1)第一年年终的总资金=第一年初投入×(1+年获利率),依此列式计算即可求解;
(2)设第一年的年获利率为p,则第二年年终的总资金可表示为:50(1+p)(1+p+10%),根据题意可得方程,解方程后舍去不合题意的解,从而得出答案.
解答 解:(1)第一年年终的总资金为50(1+p)万元;
故答案为:50(1+p);
(2)设第一年的年获利率为p,依题意,得50(1+p)(1+p+0.1)=66,
整理,得p2+2.1p-0.22=0,
解得p1=0.1,p2=-2.2 (不合题意,舍去),
答:第一年利率为10%.
点评 此题主要考查了一元二次方程的应用,弄清题意,根据题目给出的条件,找出合适的等量关系,列出方程是解题的关键.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:解答题
 如图,点A(2,6)和点B(点B在点A的右侧)都在反比例函数的图象上,点C在y轴上,BC∥x轴,tan∠ACB=2,二次函数的图象经过A、B、C三点.
如图,点A(2,6)和点B(点B在点A的右侧)都在反比例函数的图象上,点C在y轴上,BC∥x轴,tan∠ACB=2,二次函数的图象经过A、B、C三点.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 100 | B. | 200 | C. | 300 | D. | 400 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
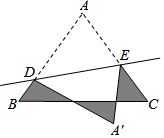 如图,等边△ABC的边长是5,D、E分别是边AB、AC上的点,将△ADE沿直线DE折叠,点A落在A′处,且点A′在△ABC外部,则阴影图形的周长为15.
如图,等边△ABC的边长是5,D、E分别是边AB、AC上的点,将△ADE沿直线DE折叠,点A落在A′处,且点A′在△ABC外部,则阴影图形的周长为15.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
| a | 0.000001 | 0.001 | 1 | 1000 | 1000000 |
| $\root{3}{a}$ | 0.01 | 0.1 | 1 | 10 | 100 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com