
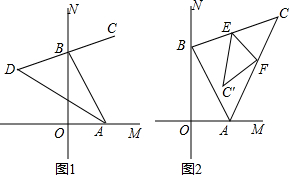
分析 (1)①根据角平分线的定义得到∠DAB=$\frac{1}{2}$∠OAB=30°,∠ABC=$\frac{1}{2}$∠ABN=75°,根据三角形的外角的性质计算即可;
②仿照①的作法计算即可;
(2)根据三角形内角和定理得到∠CAB+∠CBA=135°,根据翻转变换的性质、三角形内角和定理计算即可.
解答 解:(1)①∵∠ABO=30°,
∴∠OAB=60°,∠ABN=150°,
∵BC是∠ABN的平分线,AD是∠OAB的平分线,
∴∠DAB=$\frac{1}{2}$∠OAB=30°,∠ABC=$\frac{1}{2}$∠ABN=75°,
∴∠ADB=∠ABC-∠DAB=45°,
故答案为:45;
②设∠ABO=α,
∵∠MON=90°,
∴∠BAD=45°-$\frac{α}{2}$,∠ABC=90°-$\frac{α}{2}$,
∴∠ABD=180°-∠ABC=90°+$\frac{α}{2}$,
∴∠ADB=180°-∠BAD-∠ABD=45°;
(2)∵∠MON=90°,
∴∠ABO+∠BAO=90°,
∴∠CAB+∠CBA=$\frac{1}{2}$(∠BAM+∠ABN)=135°,
∴∠C=45°,
∴∠CEC′+∠CFC′=2(180°-∠C)=270°,
∴∠BEC′+∠AFC′=360°-(∠CEC′+∠CFC′)=90°.
点评 本题考查的是角平分线的定义、三角形内角和定理、三角形的外角的性质,掌握三角形内角和等于180°、翻转变换的性质是解题的关键.


 53随堂测系列答案
53随堂测系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 问题探索:在坐标平面内描出点A(2,0),B(4,0),C(-1,0),D(-3,0).
问题探索:在坐标平面内描出点A(2,0),B(4,0),C(-1,0),D(-3,0).查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 我县参加期中考试的所有八年级学生是总体 | |
| B. | 每位学生的数学成绩是个体 | |
| C. | 抽取的500名学生是样本容量 | |
| D. | 被抽取的500名学生是总体的一个样本 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com