
| A. | (x+$\frac{2}{5}$)2-$\frac{37}{25}$=0 | B. | 3(x+$\frac{2}{5}$)2-$\frac{37}{25}$=0 | C. | (x-$\frac{2}{5}$)2-$\frac{37}{25}$=0 | D. | 3(x-$\frac{2}{5}$)2-$\frac{37}{25}$=0 |
分析 等式左边配方时,可先提取二次项系数,然后将括号内进行配方,就可解决问题.
解答 解:∵3x2-$\frac{12}{5}$x-1=3(x2-$\frac{4}{5}$x)-1
=3(x2-$\frac{4}{5}$x+$\frac{4}{25}$-$\frac{4}{25}$)-1
=3[(x-$\frac{2}{5}$)2-$\frac{4}{25}$)]-1
=3[(x-$\frac{2}{5}$)2-$\frac{12}{25}$-1
=3(x-$\frac{2}{5}$)2-$\frac{37}{25}$,
∴方程3x2-$\frac{12}{5}$x-1=0可变形为3(x-$\frac{2}{5}$)2-$\frac{37}{25}$=0.
故选D.
点评 本题主要考查了配方法在解一元二次方程中的应用,ax2+bx+c=a(x2+$\frac{b}{a}$x+$\frac{{b}^{2}}{4{a}^{2}}$-$\frac{{b}^{2}}{4{a}^{2}}$)+c=a(x+$\frac{b}{2a}$)2-$\frac{{b}^{2}}{4a}$+c=a(x+$\frac{b}{2a}$)2+$\frac{{4ac-b}^{2}}{4a}$.


科目:初中数学 来源: 题型:选择题
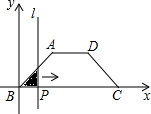 如图,在四边形ABCD中,AD∥BC,AB=DC,以点B为原点,BC边所在的直线为x轴建立平面直角坐标系,直线l与y轴重合且向右平移,若其扫过的面积(阴影部分)为S,设向右平移的距离BP为x,则S关于x的函数图象大致是( )
如图,在四边形ABCD中,AD∥BC,AB=DC,以点B为原点,BC边所在的直线为x轴建立平面直角坐标系,直线l与y轴重合且向右平移,若其扫过的面积(阴影部分)为S,设向右平移的距离BP为x,则S关于x的函数图象大致是( )| A. | 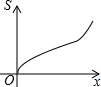 | B. |  | C. | 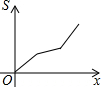 | D. | 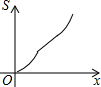 |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | $\sqrt{2}$+$\sqrt{3}$=$\sqrt{5}$ | B. | $\frac{2x{y}^{2}}{4{x}^{2}y}$=$\frac{1}{2}$ | C. | $\frac{n}{m}$=$\frac{n-a}{m-a}$ | D. | 若a>0,则$\sqrt{a^2}=a$ |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com