
 如图,已知OC是∠AOB的平分线,点P在OC上,且OP=2厘米,∠AOB=60°,过点P的动直线交OA于点D,交OB于E,那么
如图,已知OC是∠AOB的平分线,点P在OC上,且OP=2厘米,∠AOB=60°,过点P的动直线交OA于点D,交OB于E,那么| 1 |
| OD |
| 1 |
| OE |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| ||
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| ||
| 2 |
| 1 |
| OD |
| 1 |
| OE |
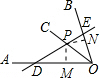 解:如图,过点P作PM⊥OD于M,PN⊥OE于N,
解:如图,过点P作PM⊥OD于M,PN⊥OE于N,| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| ||
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| ||
| 2 |
| ||
| 2 |
| 1 |
| OD |
| 1 |
| OE |
| ||
| 2 |
| ||
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| ||
| 2 |


科目:初中数学 来源: 题型:
 现有一个顶角为36°的等腰三角形,将其分割成4个等腰三角形(根据要求画出图形,标出底角度数),4个等腰三角形满足如下各自条件:
现有一个顶角为36°的等腰三角形,将其分割成4个等腰三角形(根据要求画出图形,标出底角度数),4个等腰三角形满足如下各自条件:查看答案和解析>>
科目:初中数学 来源: 题型:
 有一个进、出水管的容器,某时刻起4分钟只开进水管,此后进水管,出水管同时开放,经过8分钟注满容器,随后只开出水管,得到时间x(分钟)与水量y(升)之间的函数关系如图,那么容器的容积为
有一个进、出水管的容器,某时刻起4分钟只开进水管,此后进水管,出水管同时开放,经过8分钟注满容器,随后只开出水管,得到时间x(分钟)与水量y(升)之间的函数关系如图,那么容器的容积为查看答案和解析>>
科目:初中数学 来源: 题型:

查看答案和解析>>
科目:初中数学 来源: 题型:
 如图,要把一块含30°的直角三角板按要求分割成大小形状都相同的图形 (标注必要角度)
如图,要把一块含30°的直角三角板按要求分割成大小形状都相同的图形 (标注必要角度)查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com