
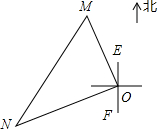
 一艘轮船和一艘渔船同时沿各自的航向从港口O出发,如图所示,轮船从港口O沿北偏西20°的方向行60海里到达点M处,同一时刻渔船已航行到与港口O相距80海里的点N处.若M,N两点相距100海里,则∠NOF的度数为70°.
一艘轮船和一艘渔船同时沿各自的航向从港口O出发,如图所示,轮船从港口O沿北偏西20°的方向行60海里到达点M处,同一时刻渔船已航行到与港口O相距80海里的点N处.若M,N两点相距100海里,则∠NOF的度数为70°. 科目:初中数学 来源: 题型:选择题
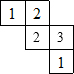 由一些大小相同的小正方体搭成的几何体的俯视图如图所示,其中正方形中的数字表示该位置上的小正方体的个数,那么该几何体的主视图是( )
由一些大小相同的小正方体搭成的几何体的俯视图如图所示,其中正方形中的数字表示该位置上的小正方体的个数,那么该几何体的主视图是( )| A. | 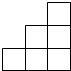 | B. |  | C. | 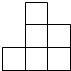 | D. | 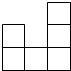 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| 金额/元 | 5 | 10 | 20 | 50 | 100 |
| 人数 | 4 | 16 | 15 | 9 | 6 |
| A. | 10,20.6 | B. | 20,20.6 | C. | 10,30.6 | D. | 20,30.6 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
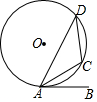 如图,$\widehat{AC}$=$\widehat{DC}$,AC平分∠DAB.
如图,$\widehat{AC}$=$\widehat{DC}$,AC平分∠DAB.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
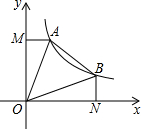 如图,一次函数y=-x+b(b>0)的图象与反比例函数y=$\frac{k}{x}$(x>0)的图象交于A、B两点,连接OA、OB,AM⊥y轴,BN⊥x轴,垂足分别为M、N.下列结论:
如图,一次函数y=-x+b(b>0)的图象与反比例函数y=$\frac{k}{x}$(x>0)的图象交于A、B两点,连接OA、OB,AM⊥y轴,BN⊥x轴,垂足分别为M、N.下列结论:| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
| 组别 | 正确字数x | 人数 |
| A | 0≤x<8 | 10 |
| B | 8≤x<16 | 15 |
| C | 16≤x<24 | 25 |
| D | 24≤x<32 | m |
| E | 32≤x<40 | n |

查看答案和解析>>
科目:初中数学 来源: 题型:解答题
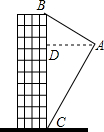 如图,航拍无人机从点A处测得一幢建筑物顶部B的仰角为32°,测得底部C的仰角为62°,此时航拍无人机与该建筑物的水平距离AD为54米,求该建筑物的高度BC(精确到0.1米,参考数据:sin 32°=0.530,cos32°=0.848,tan32°=0.625,sin 62°=0.883,cos62°=0.469,tan62°=1.88)
如图,航拍无人机从点A处测得一幢建筑物顶部B的仰角为32°,测得底部C的仰角为62°,此时航拍无人机与该建筑物的水平距离AD为54米,求该建筑物的高度BC(精确到0.1米,参考数据:sin 32°=0.530,cos32°=0.848,tan32°=0.625,sin 62°=0.883,cos62°=0.469,tan62°=1.88)查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com