
【题目】如图,某市有一块长为(3a+b) 米,宽为(2a+b)米的长方形地块,规划部门计划将阴影部分进行绿化,中间将修建一座雕像.
(1)试用含a,b的代数式表示绿化的面积是多少平方米?
(2)若a=10,b=8,且每平方米造价为100元求出绿化需要多少费用.
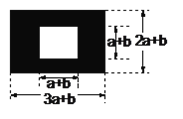
 开心试卷期末冲刺100分系列答案
开心试卷期末冲刺100分系列答案 双基同步导航训练系列答案
双基同步导航训练系列答案 黄冈小状元同步计算天天练系列答案
黄冈小状元同步计算天天练系列答案科目:初中数学 来源: 题型:
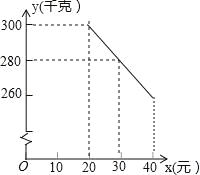
【题目】(2016云南省第22题)草莓是云南多地盛产的一种水果,今年某水果销售店在草莓销售旺季,试销售成本为每千克20元的草莓,规定试销期间销售单价不低于成本单价,也不高于每千克40元,经试销发现,销售量y(千克)与销售单价x(元)符合一次函数关系,如图是y与x的函数关系图象.
(1)求y与x的函数解析式(也称关系式)
(2)设该水果销售店试销草莓获得的利润为W元,求W的最大值.
查看答案和解析>>
科目:初中数学 来源: 题型:
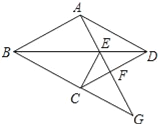
【题目】如图,四边形ABCD是菱形,点G是BC延长线上一点,连结AG,分别交BD、CD于点E、F,连结CE.
(1)求证:∠DAE=∠DCE;
(2)当CE=2EF时,EG与EF的等量关系是 .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(2016湖南省岳阳市第24题)如图①,直线y=![]() x+4交于x轴于点A,交y轴于点C,过A、C两点的抛物线F1交x轴于另一点B(1,0).
x+4交于x轴于点A,交y轴于点C,过A、C两点的抛物线F1交x轴于另一点B(1,0).
(1)求抛物线F1所表示的二次函数的表达式;
(2)若点M是抛物线F1位于第二象限图象上的一点,设四边形MAOC和△BOC的面积分别为S四边形MAOC和S△BOC,记S=S四边形MAOC﹣S△BOC,求S最大时点M的坐标及S的最大值;
(3)如图②,将抛物线F1沿y轴翻折并“复制”得到抛物线F2,点A、B与(2)中所求的点M的对应点分别为A′、B′、M′,过点M′作M′E⊥x轴于点E,交直线A′C于点D,在x轴上是否存在点P,使得以A′、D、P为顶点的三角形与△AB′C相似?若存在,请求出点P的坐标;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(2016广东省深圳市第23题)如图,抛物线![]() 与
与![]() 轴交于A、B两点,且B(1 , 0)。
轴交于A、B两点,且B(1 , 0)。
(1)、求抛物线的解析式和点A的坐标;
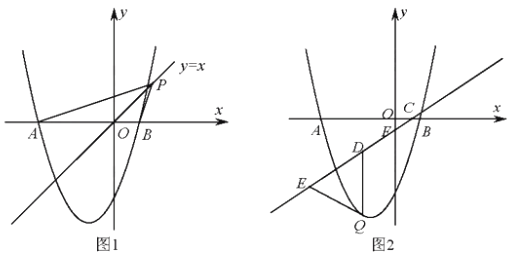
(2)、如图1,点P是直线![]() 上的动点,当直线
上的动点,当直线![]() 平分∠APB时,求点P的坐标;
平分∠APB时,求点P的坐标;
(3)如图2,已知直线![]() 分别与
分别与![]() 轴
轴 ![]() 轴 交于C、F两点。点Q是直线CF下方的抛物线上的一个动点,过点Q作
轴 交于C、F两点。点Q是直线CF下方的抛物线上的一个动点,过点Q作 ![]() 轴的平行线,交直线CF于点D,点E在线段CD的延长线上,连接QE。问以QD为腰的等腰△QDE的面积是否存在最大值?若存在,请求出这个最大值;若不存在,请说明理由。
轴的平行线,交直线CF于点D,点E在线段CD的延长线上,连接QE。问以QD为腰的等腰△QDE的面积是否存在最大值?若存在,请求出这个最大值;若不存在,请说明理由。
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某地连续九天的最高气温统计如下表:
最高气温(℃) | 22 | 23 | 24 | 25 |
天数 | 1 | 2 | 2 | 4 |
则这组数据的中位数与众数分别是( )
A.24,25
B.24.5,25
C.25,24
D.23.5,24
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如果将抛物线y=x2+2先向左平移1个单位,再向下平移2个单位,那么所得新抛物线的表达式是( )
A.y=(x﹣1)2
B.y=(x+1)2
C.y=x2+1
D.y=x2+3
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,AB=AC,AB的垂直平分线交AB于M,交AC于N.
(1)若∠ABC=70°,则∠MNA的度数是__.
(2)连接NB,若AB=8cm,△NBC的周长是14cm.
①求BC的长;
②在直线MN上是否存在P,使由P、B、C构成的△PBC的周长值最小?若存在,标出点P的位置并求△PBC的周长最小值;若不存在,说明理由.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com