
【题目】如图,某校综合实践活动小组的同学欲测量公园内一棵树DE的高度.他们在这棵树正前方一座楼亭前的台阶上A点处测得树顶端D的仰角为30°,朝着这棵树的方向走到台阶下的点C处,测得树顶端D的仰角为60°.已知A点的高度AB为2米,台阶AC的坡度为1:![]() (即AB:BC=1:
(即AB:BC=1:![]() ),且B、C、E三点在同一条直线上.请根据以上条件求出树DE的高度(测倾器的高度忽略不计).
),且B、C、E三点在同一条直线上.请根据以上条件求出树DE的高度(测倾器的高度忽略不计).

【答案】解:因为直角三角形ABC中,BC=![]() ,AB=4, 所以BC=4
,AB=4, 所以BC=4![]() ,设DF=x,
,设DF=x,
在直角三角形AFD中,

![]() ,
,
在直角三角形DCE中,
![]() ,
,
所以![]()
所以DE=![]() 米。
米。
【解析】试题分析:由于AF⊥AB,则四边形ABEF为矩形,设DE=x,在Rt△CDE中,CE═![]() =
=![]() =
=![]() ,在Rt△ABC中,得到
,在Rt△ABC中,得到![]() ,求出BC,在Rt△AFD中,求出AF,由AF=BC+CE即可求出x的长.
,求出BC,在Rt△AFD中,求出AF,由AF=BC+CE即可求出x的长.
试题解析:∵AF⊥AB,AB⊥BE,DE⊥BE,
∴四边形ABEF为矩形,
∴AF=BE,EF=AB=2
设DE=x,在Rt△CDE中,CE=![]() =
=![]() =
=![]() ,
,
在Rt△ABC中,
∵![]() ,AB=2,
,AB=2,
∴BC=2![]() ,
,
在Rt△AFD中,DF=DE-EF=x-2,
∴AF=![]() ,
,
∵AF=BE=BC+CE.
∴![]() ,
,
解得x=6.
答:树DE的高度为6米.


科目:初中数学 来源: 题型:
【题目】若二次函数y=﹣x2+4x+c的图象经过A(1,y1),B(﹣1,y2),C(2+ ![]() ,y3)三点,则y1、y2、y3的大小关系是( )
,y3)三点,则y1、y2、y3的大小关系是( )
A. y1<y2<y3 B. y1<y3<y2 C. y2<y3<y1 D. y2<y1<y3
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(1)化简:[x(x2y2﹣xy)﹣2y(x2﹣x3y)]÷3x2y
(2)化简求值:(x+2y)2﹣(x﹣2y)2﹣(x+2y)(x﹣2y)﹣4y2,其中y=1,x=![]() .
.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列命题中正确的有( ).
①已知任意一边和一个锐角对应相等的两个直角三角形全等.
②任意两角和一边对应相等的两个三角形全等.
③已知任意两边和一角对应相等的两个三角形全等.
④已知腰和顶角对应相等的两个等腰三角形全等.
⑤如果两个三角形有两条边及其中一边上的中线分别相等,那么这两个三角形全等.
A.1个B.2个C.3个D.4个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,AB=2,BC=4,其两条外角平分线AD、CD交于点D,且∠ADC=45°,连接BD交AC于点P,过点P作PE⊥AC交BC于点F,交AB的延长线于点E.
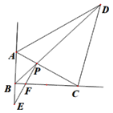
(1)求证:∠ABC=90° ;
(2)求S△PFC:S△PBF的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】 (1)如图1,等腰Rt△ABC中,∠CAB=90°,点H在BC边上,连AH,作等腰Rt△HFA,∠HFA=90°求证:AF=CF.
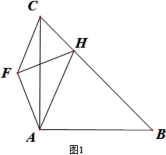
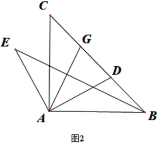
(2)如图2,等腰Rt△ABC中,∠CAB=90°,D在BC上,AD⊥AE,AD=AE,G为CD中点,求证:AG⊥BE
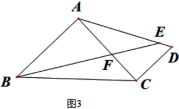
(3)如图3,等腰Rt△ABC中,∠BAC=90°,过C作CD∥AB, CD=8,连AD,在AD上取一点E使AE=AB,连BE交AC于F,若AF=9,则AD= .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平行四边形ABCD中,AE⊥BC于E,AF⊥CD于F,且∠EAF=60°,BE=2cm,DF=3cm,试求平行四边形ABCD的周长及面积.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com